NuCypher 是一個滿久的項目了，最主要的目標是為隱私保護的應用提供基礎設施，包含了 Secret Management、Dynamic Access Control 與 Secure Computation。其中會用到的代理重加密這個功能，這篇文章將介紹 NuCypher 使用的代理重加密方法，他們命名為 Umbral，在西班牙文中這是 Threshold 的意思。

簡介代理重加密與 Umbral

Umbral 是一個門檻式代理重加密方法，首先我們需要先了解重加密是什麼。在現代生活中，雲端硬碟大概是絕大多數人都會使用到的服務，也經常會拿來做文件分享等等。而若今天我們需要提供一個文件給朋友，我們通常會上傳並建立一個連結，但更機密的資料我們可能就需要先加密再上傳，以保證服務商無法竊取或流出這個資料。然而加密之後，如果想要提供給另外一個人但不同密碼，我們就需要建立許多份副本。代理重加密則將這個過程交給雲端服務商，我們將一份加密的檔案上傳後，這些服務商透過重加密來產生對不同人的加密副本，就可以使我們避免重複加密。

在上面的流程中，我們可以分成三個角色：

1. 加密方（Delegator）
2. 解密方（Delegatee）
3. 服務方（Proxy）

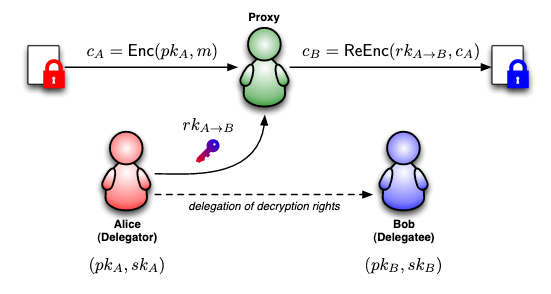加密方會提供一個重加密密鑰 rk 給服務方，服務方可以拿著加密方產生的密文 c_a 和這把 rk 去重新加密成給別人的密文 c_b，這套流程就稱作代理重加密。

代理重加密上有三個屬性：

1. Directionality：如果服務方只能利用 rk 將 c_a 轉換成 c_b，稱為 unidirectional，如果可以反過來則稱為 bidirectional。在代理重加密上，我們會希望他是 unidirectional 的，以避免解密方在使用他的密鑰產生密文後，被服務方與加密方共謀而洩漏其中的明文。
2. Number of Hops：如果服務方對於 c_a，在具備不同 rk 下（例如給 Bob 和 Charlie 的）可以分別產生對應的 c_? 則稱為 multi-hop/multi-use，否則稱為 single-hop/single-use。
3. Interactivity：如果解密方的密鑰不需參與重加密密鑰的產生流程，則稱為 non-interactive，否則為 interactive。

對於這三個屬性，Umbral 是 unidirectional、multi-hop、non-interactive 的，此外，他也引入了非互動式零知識證明來提供重加密的可驗證性。

而 Umbral 的另一個特點，就是他是門檻式（Threshold）的，在前面的的簡介中只有一個 Proxy，一旦這個 Proxy 故障，那加密方與解密方就無法完成傳遞，因此透過 Threshold 的設計，例如可以建立一個 t of N 的代理重加密會話，只要 N 個 Proxy 有 t 個正常運作就可以確保傳遞順暢。

KEM/DEM Approach

Umbral 參考了美國國家標準協會提出的 ECIES-KEM，用到了稱為 KEM/DEM Approach 的方法。KEM/DEM Approach 是一種混合加密方式，透過混合非對稱與對稱加密，來提供足夠的安全性與加解密效率（非對稱的加解密通常較為耗能）。KEM Key Encapsulate Mechanism 會先產生一個對稱加密的密鑰，再透過 DEM Data Encapsulate Mechanism 則將傳遞的資料加密。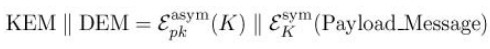

Shamir’s Secret Sharing

Umbral 中的 Threshold 特性透過 Shamir’s Secret Sharing 的方式來達成。Kimi 老師有一篇文在說這個，這邊就不展開了。

Implementation

https://github.com/nucypher/pyUmbral

Umbral 如何運作

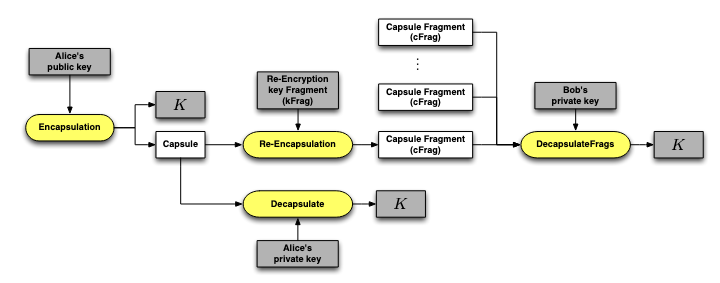這邊的 Alice 是上面的 Delegator，Bob 是 Delegatee。首先 Alice 會透過 Encapsulate 去產生對稱密鑰 K 和 Capsule，這個 Capsule 包含了讓 Bob 拿到 K 的資訊。接著 Alice 會對 Bob 產生 N 個 kFrag 並發送給 Proxy 們，Proxy 拿著 Capsule 和 kFrag 就可以產生 cFrag 並發送給 Bob，Bob 拿到 t 個 cFrag 就可以用自己的密鑰重組並解密出 K。

產生公開參數

首先會先產生一組 Parameter：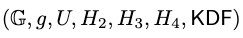

其中 G 是一個 order 為質數 q 的循環群，g 和 U 則是在 G 上的兩個 Generator。H_2, H_3, H_4 則是作為隨機數產生器雜湊函數。KDF 是 Key Derivation Function，將用這個來產生對稱密鑰。q 和 KDF 的輸出長度是這個協議的安全性參數。

KeyGen

Alice 會產生自己的非對稱密鑰對 (pk, sk) = (g^a, a)，接著產生提供給 Proxy 的 kFrag。產生 kFrag 的步驟如下：

1. Alice 會選擇一個暫時的非對稱密鑰對 (x_A, X_A = g^{x_A})，這裡可能是考慮 Alice 和 Bob 會需要建立不只一次協議
2. 將這個密鑰對和 Bob 做非互動式 Diffie-Hellman 密鑰交換，計算 d = H_3(X_A, pk_B, (pk_B)^{x_a})
3. 依照 Shamir’s Secret Sharing 的方式，產生一個 t-1 次的多項式 f，其中秘密 f_0 = a \cdot d^{-1} \bmod q
4. 計算共有的 Index D = H_6(pk_A, pk_B, pk_B^a)
5. 產生 N 個 kFrag：
   5.1 選取隨機數 id \in \Z_q
   5.2 計算 Shamir’s Secret Sharing 上的點 s_x = H_5(id, D)
   5.3 計算 Re-encrypt Key rk = f(s_x)
   5.4 計算 Commitment U_1 = U^{rk}
   5.5 組合成 kFrag (id, rk, X_A, U_1)

在產生 kFrag 中，論文有提到 z_1, z_2，這兩個是作為驗證用的，在官方實作上是讓 Alice 對 kFrag 加上 pk_A, pk_B 做簽章來提供驗證功能，由於這兩個沒有參與後面的運算這邊選擇略過。

產生 Capsule

Alice 會選擇兩個隨機數 r, u \in \Z_q，並包裝成 (E, V, s) = (g^r, g^u, u + r \cdot H_2(E, V))。對稱密鑰則透過 KDF((pk_A)^{r+u}) 得出，任何人收到 Capsule 都可以透過 g^s \stackrel{?}{=} V \cdot E^{H_2(E,V)} 去檢驗 E, V 的正確性。而 Alice 可以拿 Capsule 和 Private Key a 去取回 K = KDF((E \cdot V)^a)。

重加密與解密

Proxy 拿到 Capsule 和 kFrag 後，就可以產生 cFrag：(E_1, V_1, id, X_A) = (E^{rk}, V^{rk}, id, X_A)。同時還會產生 NIZK 證明：

1. 隨機選擇 \tau \in \Z_q
2. 計算 (E_2, V_2, U_2) = (E^\tau, V^\tau, U^\tau)
3. 計算 h = H(E, E_1, E_2, V, V_1, V_2, U, U_1, U_2, \text{aux})
4. 計算 \rho = \tau + h \cdot rk
5. 發送 \pi = (E_2, V_2, U_2, U_1, z_1, z_2, \rho, \text{aux})

這可能是基於 NuCypher 設計 Stake 機制，透過這個 NIZK，網路可以透過計算 E^\rho = E_2 \cdot E_1^h 驗證這個 Proxy 有沒有正確的計算而無需取得 rk

Bob 蒐集足夠的 cFrag 後，就可以來做解密，步驟如下：

1. 計算 D = H_6(pk_A, pk_B, pk_A^b)（即 KeyGen 4. 於 Bob 方的運算）和 d = H_3(X_A, pk_B, (X_a)^{b})（即 KeyGen 2. 於 Bob 方的運算）。
2. 對每個 cFrag 計算對應的 s_i 與\lambda_i = \displaystyle\prod_{j=1,j \ne i}^{t} \frac{s_{i}}{s_j-s_i}
3. 計算 E' = \displaystyle\prod_{i=1}^t (E_{1,i})^{\lambda_{i}} 與 V' = \displaystyle\prod_{i=1}^t (V_{1,i})^{\lambda_{i}}
4. 計算K = KDF((E' \cdot V')^d)

這邊用我自己比較好理解的方式去寫，所以可能有點 Bug。其中如果把 E' 展開，可以得到 E'=\prod_{i=1}^t(E_{1,i})^{\lambda_{i,s}}=\prod_{i=1}^tE^{rk_i\lambda_{i,s}}=\prod_{i=1}^tE^{f(s_x,i)\lambda_{i,s}}=E^{\sum_{i=1}^tf(s_{x,i})\lambda_{i,s}}=E^{f(0)}=E^{ad^{-1}}，這裡做的就是前面 KeyGen 5. 透過 Shamir’s Secret Sharing 的還原。套回 4. 後可以看出他與產生 Capsule 一節中最後的相同，從而使 Alice 與 Bob 共享這個 Key。

傳遞密文

最後再使用 KEM/DEM Approach 的方式來傳遞密文就可以達成完整的 Re-Encryption。原先產生 Capsule 時，會同時產生密文 encData = SymEncrypt_K(message)，並傳遞 C = (Capsule, encData)，當 Bob 拿到時先解出 K 再 message = SymDecrypt(encData) 即可。

Reference

[1] https://raw.githubusercontent.com/nucypher/umbral-doc/master/umbral-doc.pdf