上個月 Vitalik 寫了一篇文講 Verkle Tree,對於區塊鏈技術熟悉的人,大概會很快聯想到 Merkle Tree,也確實,Verkle Tree 就是 Merkle Tree 的一種變形,意思是 Very Short Merkle Tree,那具體改了什麼?又有什麼好處呢?從 Very Short 上,大概就可以猜出 Verkle Tree 提供的改進就是縮短了 Merkle Tree 的某部分。在開始之前,我們先往回看 Merkle Tree 這東西。
Merkle Tree
Merkle Tree 中只有最終端的節點會攜帶資料,而這些終端節點會組成中間節點,中間節點又可以組成更上層的中間節點,最終組成最上層的根節點。其中,組成的方式就是將下層的節點合併 Hash。 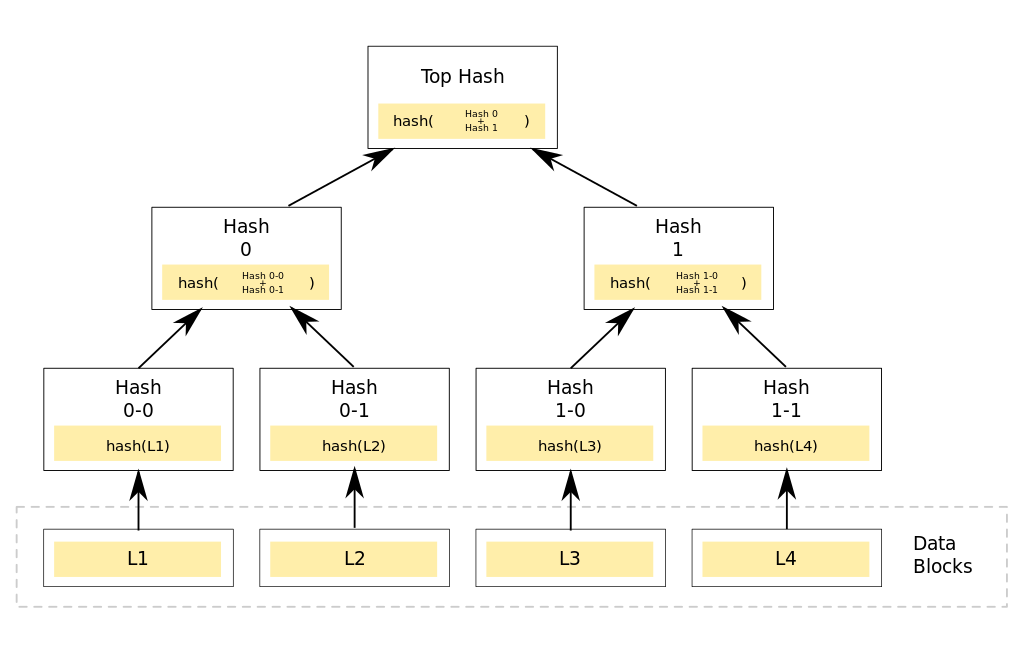 (圖取自 Wikipedia)
(圖取自 Wikipedia)
Merkle Tree 的好處在於要檢查正確性時,可以更容易的找出錯誤的地方。因此常用於 P2P 下載時,檢查檔案錯誤並重新下載的階段。
Merkle Tree 與區塊鏈
在 Bitcoin 中,Merkle Tree 用於記錄打包在某一區塊中的交易,這是 Bitcoin 中一個名為 Simplified Payment Verification 的方法。透過這個方法,只要獲得了區塊的 Merkle Root 和 Merkle Path Proof,就能輕易的驗證交易是否包含在某個區塊中,使得一般人不需要下載整個網路也可以交易。而在以太坊中,則以類似方式用在交易、收據、狀態資料上。
Merkle Path Proof
這裡提到的 Merkle Path Proof 概念是:如果我想要知道某個資料是否存在這個 Merkle Tree,我只要能不斷往上驗證就可以。以上圖為例子,若我要驗證 L3 是否包含,我需要的是 Hash 1-1、Hash 0。由於我知道 L3,就能計算 Hash 1-0,再與 Hash 1-1 組合計算出 Hash 1,最後與 Hash 0 組合計算得 Top Hash。這個如果與我所知道的 Root 相同,那就代表這個 L3 確實在內,而無需去取得整個 Tree 做驗證。
由此可知,如果我要在某個 Merkle Tree 中,驗證某個資料是否存在,我需要所有到根節點間所有節點的相鄰節點 Hash。亦即對於寬度 n、深度 m 的 Merkle Tree,需要取得最多 (n - 1) * (m - 1) 個 Hash。(n - 1:相鄰節點數、m - 1:中間節點數,由於會有空節點因此通常小於此值。)
Merkle Path Proof 有什麼問題
目前以太坊基於狀態更新的需要使用了寬度 16 的 Merkle Patricia Tree,這部份暫不展開(還沒讀到)。據 Vitalik 文章所說,從具有 100 萬個資料的 Merkle Tree 產生一個資料的 Path Proof 就達到 1 kb,而若需要取得多個資料時,就會增加這個大小。相較之下,Verkle Tree 不到 300 bytes,取得多個資料時也不是線性增加的。
Verkle Tree
前面說到 Verkle Tree 就是 Very Short Merkle Tree,加上剛剛提到了 Merkle Tree 的問題,就知道接下來要解決的是這個 Path Proof 的長度問題。
Verkle Tree 如何縮短 Proof
Merkle Path Proof 中,由於每個中間節點都需要其同代相鄰節點才能提出證明,因此讓整個 Proof 長度變長。這時,有個叫做 Vector Commitment 的方法就可以派上用場。概念上,Vector Commitment 提出該節點位於同代節點集合中第某個位置的證明,因此無需傳遞其他的相鄰節點也可說服驗證者。
實際上會採用的是 Polynomial Commitment,這也是最高效率的 Vector Commitment。簡單來說,我們可以把每一層節點們的 Index 與 Hash 組出一個多項式(拉格朗日是你的好朋友),這個多項式則成為該層之上中間節點的 Hash,接著針對這個多項式與其值產生對應的 Commitment 並產生 Proof,用密碼學的手段就可以測試出某層的某個節點是否是某個 Hash。
因此,原本我們需要傳遞每一層的相鄰節點 Hash,就可以變成只傳遞一個固定大小的 Proof。
不夠,還要再短
雖然已經讓每一層只需要產生一個 Proof,但 Polynomial Commitment 的特性使整個流程可以再進一步。概念上,是將前面的所有 Commitment 再去生成一個 Commitment,這個 Commitment 就包含所有「某個節點的第?個子節點是某個節點」的關係,因此最後只會產生一個固定大小的證明。
效率如何呢
在上面從 Merkle Path Proof 到 Verkle Tree 改進中,可以看到產生 Proof 的效率與大小、驗證 Proof 的效率是重要的指標,此外,由於以太坊的狀態樹是會更新的,因此還會要考慮更新資料時的效率。
對於產生 Proof 的效率,最主要的影響在於合併階段(上一段落),但這段也只需要四個 Field Operation 乘上樹的寬度,因此寬度 256 ~ 1024 都屬於可用的範圍。大小方面,上面已經解釋如何縮短,就不再重述。對於驗證上,通常小於一百毫秒。
而更新樹時,雖然會需要更新每一層的 Commitment,但應用同態屬性後就不太是個問題。在所需的橢圓曲線乘法上,也有預計算和記錄中間值來加速的手段。
總結
根據 Vitalik 的文章,如果採用 Verkle Tree 之後,可以縮短原本的證明大小到 1/20 ~ 1/30 。但這裡有個問題:更新樹這一段使用了線性同態屬性,在量子密碼學興起後,可能有被攻破的風險,因此一旦有相關突破且沒有進一步的改進,或許還是得回歸 SNARK 化的 Merkle Tree。
寫在最後
這篇文在我的瀏覽器中待了半個月,今天心血來潮抓出來看並寫成文章,發現自己對這些東西真的好不熟悉(死),雖然知道 Merkle Tree 卻不知道到底用在哪些地方,裡面也延伸出好多要看的東西,像是 Merkle Patricia Tree 又是什麼、Kate Commitment 和 Bulletproof Commitment(糟糕,明明我聽過別人介紹)。Merkle Tree 設計上似乎更著重在整體的正確性,但區塊鏈應用上更多時候只需要一部分(可能極小)內容,因此 Verkle Tree 就會更好,或許還有其他部分有類似的改進可能也說不定?