Building a Witness Encryption with Groth16

(Trigger warning: This article contains heavy mathematics and cryptography.)

Witness Encryption is a type of encryption scheme characterized by using an NP Statement for encryption and the corresponding Witness for decryption. Groth16 is a classical zkSNARK scheme that allows one party to prove that a Statement and Witness pair satisfies a specific NP relation. The Groth16 scheme is based on the Circuit Satisfiability Problem (CircuitSAT), which is NP-complete, so any NP problem can be reduced to this problem and then use Groth16 to establish zkSNARK provers and verifiers. Based on this, we can attempt to transform Groth16 into a Witness Encryption, that is, construct a Witness Encryption based on CircuitSAT, thereby enabling us to perform encryption and decryption using arbitrary NP problems.

This article is an excerpt and security proof correction of my master’s thesis “Witness Encryption Scheme for Quadratic Arithmetic Programs“.

中文版 | 日本語 | English

Background Knowledge

Before explaining the construction method, I will introduce some background knowledge. Those confident in their understanding can proceed directly to the Construction section. Here we will omit detailed mathematical knowledge about elliptic curve cryptography, bilinear mapping groups, etc. (Extended reading: Exploring Elliptic Curve Pairings). We will use the same notation as the Groth16 paper, expressing group elements and pairing computations as $[a]_1\cdot[b]_2 = [c]_T$.

Witness Encryption

Witness Encryption was proposed by Garg et al. in 2013. For an NP Language $\mathcal{L}$, an encryptor can encrypt through a Statement $x$, and a decryptor decrypts through a Witness $w$, where $(x, w) \in R_\mathcal{L}$. For example, we can use Sudoku rules to construct a Relation and use Witness Encryption to establish an encryption system that encrypts using Sudoku puzzles, and those who solve the puzzle can decrypt.

Since Witness Encryption is constructed based on NP problems, we can use real-world verification problems to construct a Relation, and if we can establish a Witness Encryption scheme based on this, we can design encryption and decryption systems more freely. For example, in application scenarios where NFTs serve as content ownership, we want only holders of specific NFTs to be able to decrypt content. We can use the NFT’s contract address and Token ID as the Statement, and the valid state of the blockchain along with the holder’s identity proof (such as signatures) as the Witness to achieve our requirements.

Witness Key Encapsulation Mechanism

Key Encapsulation Mechanism (KEM) is a common method for hybrid encryption, conceptually dividing encryption into key generation and symmetric encryption parts. Both sides first compute the same key through different methods, then use this key in symmetric encryption. This is because symmetric encryption is usually more efficient than other encryption methods (such as asymmetric encryption), and the plaintext space includes all encryptable strings. In contrast, methods like asymmetric encryption typically use limited plaintext spaces, making it difficult to specify and encrypt plaintext. Conversely, it is easier to design algorithms that allow encryptors and decryptors to compute the same key.

In recent years, many Witness Encryption designs have been proposed, and this paper uses one of these design approaches called Witness Key Encapsulation Mechanism (WKEM). WKEM was first proposed by Gwangbae Choi and Serge Vaudenay. This research also uses the same approach, designing a WKEM and combining it with a symmetric encryption scheme to construct a complete Witness Encryption.

A WKEM consists of two algorithms: $\text{Encap}, \text{Decap}$. (To simplify the explanation, unlike the original paper, we will directly use Relation $R$ here.)

$(\text{ct}, k) \leftarrow \text{Encap}(R, x)$: Input Relation and Statement, output ciphertext $\text{ct}$ and key $k$.
$k \leftarrow \text{Decap}(R, \omega, \text{ct})$: Input Relation, Witness, and ciphertext $\text{ct}$, output key $k$.

That is, the encryptor can use the Relation and Statement to first generate a key, while those with the Witness can use the ciphertext to generate the same key, thereby achieving the goal of Witness Encryption.

In WKEM, we focus on two security properties: Correctness and Extractability. Correctness means that if computed according to the correct algorithm, for valid Relation, Statement, and Witness, the same key should be output. Roughly speaking, extractability means that for decryptors who can correctly output the key, we believe they possess the correct Witness.

In this research, we use the following definition:

WKEM Extractability: If for any non-uniform stateful probabilistic polynomial time adversary and any Relation, there exists a non-uniform probabilistic polynomial time extractor, such that for some negligible function $\epsilon(\lambda)$ satisfying

$$
\text{Pr}[\text{Expt}^\text{CPA}_{\text{WKEM},\mathcal{A}}(1^\lambda, R) = 1] \geq \frac{1}{2} + \epsilon(\lambda)
$$

then for some negligible function $\delta(\lambda)$, this equation holds:

$$
\text{Pr}\left[
(x, w) \in R :
\begin{array}{r}
x \leftarrow \mathcal{A}(1^\lambda, R) \\
w \leftarrow \text{Ext}^{\mathcal{A}(\cdot, \cdot)}(R, x)
\end{array}
\right] \geq \delta(\lambda)
$$

where the second probability is sampled over the randomness of $\mathcal{A}$ and extractor $\text{Ext}$.

$\text{Expt}^\text{CPA}_{\text{WKEM},\mathcal{A}}(1^\lambda, R)$ is defined as:

$$
\begin{array}{l}
\mathbf{Expt}_{\mathsf{WKEM}, \mathcal{A}}^{\mathsf{CPA}}(1^\lambda, R) \\
\hline
x \leftarrow \mathcal{A}(1^\lambda, R) \\
b \overset{$}{\leftarrow} {0, 1} \\
(ct, k_0) \leftarrow \mathsf{Encap}(R, x) \\
k_1 \overset{$}{\leftarrow} \mathcal{K} \\
b’ \leftarrow \mathcal{A}(ct, k_b) \\
\mathbf{return} \begin{cases}
1 & \text{if } b’ = b \\
0 & \text{otherwise}
\end{cases}
\end{array}
$$

In this experiment, we provide the Relation to the adversary, who generates an arbitrary Statement. We then encrypt using this Statement and randomly send either the generated key $k_0$ or a randomly selected $k_1$ to the adversary, who must determine whether the received key is the real key or a randomly selected one. Therefore, the definition means in plain language: if there exists an adversary whose success probability is higher than random guessing, then the probability that the extractor obtains a Witness and the Statement and Witness satisfy the Relation is non-negligible.

In this article, we modify the adversary and extractor to be non-uniform, in order to align our security with Groth16’s security proof, which differs from other WKEM schemes (and the original paper). In subsequent proofs, we will combine with Groth16’s Soundness proof to complete our proof. This paper believes there exist other proof methods that can maintain uniform adversaries and extractors, but this research will not explore them.

zkSNARK

Since this research ultimately aims to construct a Witness Encryption from a zkSNARK scheme: Groth16, we will utilize some properties of zkSNARK, so we provide a brief introduction below.

zkSNARK is a type of zero-knowledge proof system with characteristics including Zero-knowledge, Succinct, Non-interactive, and is an Argument of Knowledge. Argument of Knowledge means this system allows a prover to present an argument to convince a verifier that they know certain knowledge. (Compared to Proof of Knowledge, which requires that a proof necessarily implies knowledge, Argument of Knowledge allows the prover to compute an argument with extremely small probability, making it easier to design.) Non-interactive allows the prover to give the verifier just one proof. (In contrast to Interactive Proof Systems, which may require the prover to accept challenges from the verifier and respond.) Succinct requires that the proof be more efficient than directly giving the answer, since the most direct knowledge proof is the knowledge itself. Zero-knowledge prevents the verifier from learning properties related to the knowledge itself, knowing only whether the prover possesses the knowledge.

A zkSNARK consists of four algorithms: Setup, Prove, Verify, and Simulator. Setup generates a system setup for a Relation, including public information and a trapdoor, where the trapdoor is used in the Simulator. Prove accepts Relation, public information, Statement, and Witness and outputs a proof. Verify receives Relation, public information, Statement, and proof and determines whether it holds. Simulator is used to prove zero-knowledge properties, using Relation, Statement, and trapdoor to generate simulated proofs. Due to space constraints, we will not explain the details.

In this research, the main property we need is “having a proof necessarily implies having knowledge,” whose academic term is “Soundness.” Therefore, here I will explain the specific definition:

Soundness: For all non-uniform polynomial time adversaries $\mathcal{A}$, there exists a non-uniform polynomial time extractor $\text{Ext}$ (this extractor can use all states of $\mathcal{A}$) that satisfies the following relationship:

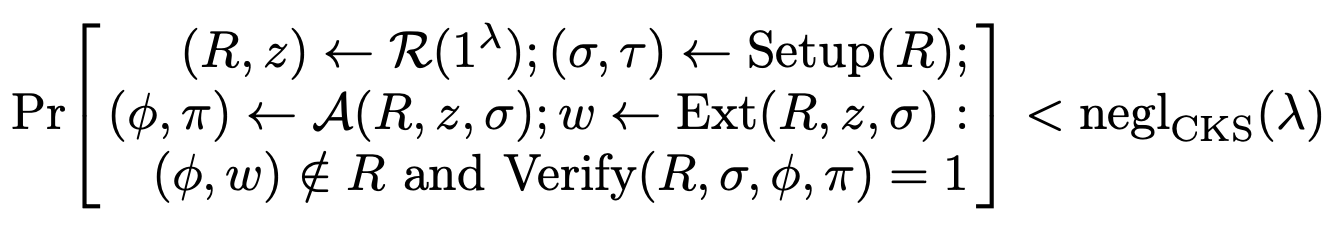
where $\text{negl}_\text{CKS}(\lambda)$ is a negligible function, $R$ is the Relation represented here by a Generator $\mathcal{R}$, $\sigma, \tau$ are information generated during system setup, $\phi$ is the Statement, $\pi$ is the Proof, and $\omega$ is the Witness.

This definition may seem difficult to understand at first glance, but simply put: if an adversary can generate a valid Statement and Proof pair, it means there exists an extractor that can use this adversary’s internal state and public information to generate a Witness that belongs to the Relation with the Statement. (So having a Proof implies having a Witness.)

Groth16

Groth16 is a representative zkSNARK scheme that accepts Quadratic Arithmetic Program (QAP) Relations in the following format:

$$
R = (p, \mathbb{G}_1, \mathbb{G}_2, \mathbb{G}_T, e, g, h, \ell, \{ u_i(X), v_i(X), w_i(X) \}^m_{i=0}, t(X))
$$

This Relation defines a bilinear mapping group and the Language of Statement and Witness as $(a_1,…, a_\ell) \in \mathbb{Z}_p^\ell$, $(a_{\ell+1},…a_m) \in \mathbb{Z}_p^{m-\ell}$, satisfying $a_0 = 1$

$$
\sum_{i=0}^{m}a_iv_i(X) \cdot \sum_{i=0}^{m}a_iv_i(X) = \sum_{i=0}^{m}a_iw_i(X) + h(X)t(X)
$$

where $h(X)$ is a quotient polynomial of degree $n−2$, and $n$ is the degree of $t(X)$.

The algorithms of Groth16 are defined as follows:

Algebraic Group Model (AGM)

The Algebraic Group Model (AGM) is a security analysis model. In this model, algorithms are algebraic. This means algorithms can perform algebraic operations on groups but must provide coefficient combinations. For example, an algorithm with inputs $[a]_1, [b]_1$ can output $2[a]_1, [a + b]_1$ because these can be expressed as coefficient combinations ($(2, 0), (1, 1)$), but it cannot output $[ab]_1$ because it cannot provide coefficients for this operation.

We use the definition proposed by Matteo Campanelli et al.:

Construction

This research uses the same WKEM-WE construction and WKEM representation as Fleischhacker et al.’s research. That research explained how to use WKEM to build Witness Encryption and proved related security properties. Therefore, we will focus here on explaining how to construct WKEM.

WKEM for QAP

We will define a WKEM based on QAP, using the same QAP format as Groth16. We define the $\text{Encap}, \text{Decap}$ algorithms as follows:

where $H$ is a Random Oracle that converts $\mathbb{G}_T$ elements into an element $k$ in the Key space.

In overview, the encryptor will pass $\sigma$ to the attempted decryptor. For the decryptor to compute $s$, they need $\{[r^2w_i(x)]_1\}^\ell_{i=0}$. Since $r$ is constrained by the discrete logarithm problem and cannot be extracted from other elements, the decryptor will need another way to compute this. (Note that in $\sigma$, information directly containing related data is limited to $i$ between $\ell+1$ and $m$.) This other way is the relationship mentioned earlier. To use this relationship, the decryptor needs the Statement and Witness.

Security Proof

As mentioned earlier, WKEM focuses on two security properties: correctness and extractability. Since correctness can be simply confirmed by checking the algorithm, this paper will not elaborate on it. Next, we will focus on proving extractability.

Let $\mathcal{A}$ be a non-uniform probabilistic polynomial time adversary satisfying

$$
\text{Pr}[\text{Expt}^\text{CPA}_{\text{WKEM},\mathcal{A}}(1^\lambda, R) = 1] \geq \frac{1}{2} + \epsilon(\lambda)
$$

We can construct an extractor. This extractor executes Groth16’s Setup algorithm to obtain $\sigma_\text{Groth16}$. Then, the extractor executes a modified $\text{Encap}$ algorithm, using from $\sigma_\text{Groth16}$:

$$
([\alpha]_1, [\beta]_1, [\beta]_2, \{[x^i]_1\}_{i=0}^{n-1}, \{[x^i]_2\}_{i=0}^{n-1})
$$

(Since Groth16’s Setup algorithm also randomly selects, this modification completely simulates the original algorithm).

Extracting Vectors

The extractor saves $s$ (hereafter using $\hat{s}$ to distinguish from the adversary’s), computes $(\text{ct}, k_0)$, and randomly selects $k_1 \leftarrow K$ (where $K$ is the Key space) and a bit $b \leftarrow \{0, 1\}$. The extractor then creates an empty list $\Gamma$. When $\mathcal{A}$ uses the Random Oracle ($H$), this extractor simulates the Random Oracle and behaves as follows based on the input value: if $s \neq \hat{s}$, the extractor checks whether $(s, k’)$ exists in $\Gamma$; if it exists, it returns $k’$, otherwise it randomly selects $k’$, stores it in $\Gamma$, and returns it. If $s = \hat{s}$, it interrupts $\mathcal{A}$ and returns $k$.

Since the adversary executes under AGM, consider the adversary’s inputs:

$$
[\mathcal{X}]_1 = ([\alpha]_1, \{[ru_i(x)]_1\}_{i=0}^m) \\
[\mathcal{Y}]_2 = ([\beta]_2, \{[rv_i(x)]_2\}_{i=0}^m) \\
[\mathcal{Z}]_T = ( \{ [r\beta u_i(x) + r\alpha v_i(x) + r^2w_i(x)]_T \}^m_{i=\ell+1}, \{ [r^2 x^i t(x)]_T \}^{n-2}_{i=0})
$$

where $[\mathcal{Z}]_T$ is obtained through the following computation:

$$
[r\beta u_i(x) + r\alpha v_i(x) + r^2w_i(x)]_T = [\frac{r\beta u_i(x) + r\alpha v_i(x) + r^2w_i(x)}{\delta}]_1 \cdot [\delta]_2 \\
[r^2 x^i t(x)]_T = [\frac{r^2 x^i t(x)}{\delta}]_1 \cdot [\delta]_2
$$

The adversary will also output vectors:

$$
((\mathcal{A}_{i,j})_{i\in[m],j\in[m]}, (\mathcal{B}_{i})_{i\in[m-\ell-1+n-2]})
$$

We note the correspondence relationship of $\mathcal{A}_{i.j}, \mathcal{B}_{i}$.

$\mathcal{A}_{0,0}$ corresponds to the coefficient of $[\alpha]_1 \cdot [\beta]_2$, fixed as 1. ${\mathcal{A}_{0,i}}_{i=0}^m$ corresponds to $\{a_i\}_{i=0}^m$ in the $B$ computation (hereafter denoted as $\{a_{B,i}\}_{i=0}^m$). $\{\mathcal{A}_{i,0}\}_{i=0}^m$ corresponds to $\{a_i\}_{i=0}^m$ in the $A$ computation (hereafter denoted as $\{a_{A,i}\}_{i=0}^m$). The remaining parts are $a_{A,i}a_{B,i}$, which will not be used subsequently and are therefore skipped.

$\{\mathcal{B}_{i}\}_{i=0}^{m-\ell-1}$ corresponds to $\{a_i\}_{i=\ell+1}^m$ in the $C$ computation (hereafter denoted as $\{a_{C,i}\}_{i=\ell+1}^m$). $\{\mathcal{B}_{i}\}_{i=m-\ell}^{m-\ell-1+n-2}$ corresponds to the coefficients of $h(x)$.

WKEM Equation Derivation

From the equality of $s$ from the Encap algorithm and the adversary’s $s$, we can derive the following equation:

$$
\begin{align*}
s = &[\alpha]_1 \cdot [\beta]_2 + \sum^\ell_{i=0} a_i[r\beta u_i(x) + r\alpha v_i(x) + r^2w_i(x)]_1 \cdot [1]_2 \\
= &([\alpha]_1 + \sum^{m}_{i=0}a_{A,i} [ru_i(x)]_1) \cdot ([\beta]_2 + \sum^{m}_{i=0}a_{B,i} [rv_i(x)]_2) \\
& - (\sum^{m}_{i=\ell+1}a_{C,i}[\frac{r\beta u_i(x) + r\alpha v_i(x)+r^2w_i(x)}{\delta}]_1 + [\frac{r^2h(x)t(x)}{\delta}]_1) \cdot [\delta]_2
\end{align*}
$$

After simplification, we get:

$$
\begin{align*}
\sum^\ell_{i=0} & a_i[r\beta u_i(x) + r\alpha v_i(x) + r^2w_i(x)]_1 \cdot [1]_2 \\
= \sum^{m}_{i=0} & a_{A,i} [ru_i(x)]_1 \cdot [\beta]_2 + \sum^{m}_{i=0} a_{B,i} [\alpha]_1 \cdot [rv_i(x)]_2 \\
& + (\sum^{m}_{i=0}a_{A,i} [ru_i(x)]_1) \cdot (\sum^{m}_{i=0}a_{B,i} [rv_i(x)]_2) \\
& - (\sum^{m}_{i=\ell+1}a_{C,i}[\frac{r\beta u_i(x) + r\alpha v_i(x)+r^2w_i(x)}{\delta}]_1 + [\frac{r^2h(x)t(x)}{\delta}]_1) \cdot [\delta]_2
\end{align*}
$$

Computing the values of both sides in $\mathbb{G}_T$:

$$
\begin{align*}
\sum^\ell_{i=0} & a_i[r\beta u_i(x) + r\alpha v_i(x) + r^2w_i(x)]_T \\
= \sum^{m}_{i=0} & a_{A,i} [r\beta u_i(x)]_T + \sum^{m}_{i=0} a_{B,i} [r\alpha v_i(x)]_T \\
& + [\sum^{m}_{i=0}a_{A,i} ru_i(x) \sum^{m}_{i=0}a_{B,i} rv_i(x)]_T \\
& - (\sum^{m}_{i=\ell+1}a_{C,i}[r\beta u_i(x) + r\alpha v_i(x)+r^2w_i(x)]_T + [r^2h(x)t(x)]_T)
\end{align*}
$$

Rearranging the equation, moving terms containing $w(x)$ to the right side and those not containing it to the left side, and dividing both sides by $r^2$:

$$
\begin{align*}
[\sum^{m}_{i=0} & a_{A,i} u_i(x) \sum^{m}_{i=0}a_{B,i} v_i(x)]_T \\
& + \sum^{m}_{i=0} a_{A,i} [\frac{\beta u_i(x)}{r}]_T + \sum^{m}_{i=0} a_{B,i} [\frac{\alpha v_i(x)}{r}]_2 \\
= \sum^\ell_{i=0} & a_i[\frac{\beta u_i(x)}{r} + \frac{\alpha v_i(x)}{r} + w_i(x)]_T \\
& + (\sum^{m}_{i=\ell+1}a_{C,i}[\frac{\beta u_i(x)}{r} + \frac{\alpha v_i(x)}{r}+w_i(x)]_T + [h(x)t(x)]_T)
\end{align*}
$$

We observe $\frac{\alpha}{r}, \frac{\beta}{r}$ and can see that these values are not equal to 0, and their coefficients are independent of other terms, so we can conclude:

$$
\sum^{m}_{i=0} a_{A,i} u_i(x) - \sum^{\ell}_{i=0} a_{i} u_i(x) - \sum^{m}_{i=\ell+1} a_{C,i} u_i(x) = 0 \\
\sum^{m}_{i=0} a_{B,i} v_i(x) - \sum^{\ell}_{i=0} a_{i} v_i(x) - \sum^{m}_{i=\ell+1} a_{C,i} v_i(x) = 0
$$

We can further rearrange the equation from the previous step to get:

$$
\begin{align*}
[\sum^{m}_{i=0} & a_{A,i} u_i(x) \sum^{m}_{i=0}a_{B,i} v_i(x)]_T \\
& = \sum^\ell_{i=0} a_i[w_i(x)]_T + (\sum^{m}_{i=\ell+1}a_{C,i}[w_i(x)]_T + [h(x)t(x)]_T)
\end{align*}
$$

Extractor Constructs Groth16 Proof

After the extractor obtains these coefficients from the adversary, it can construct a Groth16 Proof $[A’]_1, [B’]_2, [C’]_1$

$$
\begin{align*}
A’ &= \alpha + \sum_{i=0}^m a_{A,i} u_i(x) + r’ \delta’ \\
B’ &= \beta + \sum_{i=0}^m a_{B,i} v_i(x) + s’ \delta’ \\
C’ &= \sum_{i=\ell+1}^m \frac{ a_{C,i} (\beta u_i(x) + \alpha v_i(x) + w_i(x)) + h(x) t(x)}{\delta’} + s’A + r’B - r’s’\delta’
\end{align*}
$$

Here $r’, s’, \delta’$ are from $\sigma_\text{Groth16}$. We substitute these three elements into Groth16’s Verify algorithm:

$$
\begin{align*}
[A’]_1 \cdot &[B’]_2 = \\
& [\alpha]_1 \cdot [\beta]_2 + \sum_{i=0}^{\ell} a_i \left[ \frac{\beta u_i(x) + \alpha v_i(x) + w_i(x)}{\gamma} \right]_1 \cdot [\gamma]_2 + [C’]_1 \cdot [\delta’]_2
\end{align*}
$$

After expansion, we get: (To avoid overly long expressions, the last line is not expanded here. In brief, this line eliminates the $r’\delta’, s’\delta’$ parts in $A’, B’$.)

$$
\begin{align*}
([\alpha]_1 + & \sum_{i=0}^m a_{A,i} [u_i(x)]_1 + r [\delta’]_1) \cdot ([\beta]_2 + \sum_{i=0}^m a_{B,i} [v_i(x)]_2 + s [\delta’]_2) = \\
[\alpha]_1 &\cdot [\beta]_2 + \sum_{i=0}^{\ell} a_i \left[ \frac{\beta u_i(x) + \alpha v_i(x) + w_i(x)}{\gamma} \right]_1 \cdot [\gamma]_2 \\
& + (\sum_{i=\ell+1}^m [\frac{ a_{C,i} (\beta u_i(x) + \alpha v_i(x) + w_i(x)) + h(x) t(x)}{\delta}]_1) \cdot [\delta’]_2 \\
& + (s’[A]_1 + r’[B]_1 - [r’s’\delta’]_1) \cdot [\delta’]_2
\end{align*}
$$

After canceling equal values on both sides, we get:

$$
\begin{align*}
(\sum_{i=0}^m a_{A,i} & [u_i(x)]_1) \cdot (\sum_{i=0}^m a_{B,i}[v_i(x)]_2) \\
& + \sum_{i=0}^m a_{B,i} [\alpha]_1 \cdot [v_i(x)]_2 + \sum_{i=0}^m a_{A,i} [u_i(x)]_1 \cdot [\beta]_2 = \\
\sum_{i=0}^{\ell} a_i & \left[ \frac{\beta u_i(x) + \alpha v_i(x) + w_i(x)}{\gamma} \right]_1 \cdot [\gamma]_2 \\
& + (\sum_{i=\ell+1}^m [\frac{ a_{C,i} (\beta u_i(x) + \alpha v_i(x) + w_i(x)) + h(x) t(x)}{\delta}]_1) \cdot [\delta’]_2
\end{align*}
$$

Computing the values of both sides in $\mathbb{G}_T$:

$$
\begin{align*}
[\sum_{i=0}^m & a_{A,i} u_i(x) \sum_{i=0}^m a_{B,i}v_i(x)]_T + \sum_{i=0}^m a_{B,i} [\alpha v_i(x)]_T + \sum_{i=0}^m a_{A,i} [\beta u_i(x)]_T \\
= & \sum_{i=0}^{\ell} a_i \left[ \beta u_i(x) + \alpha v_i(x) + w_i(x) \right]_T \\
& + \sum_{i=\ell+1}^m [a_{C,i} (\beta u_i(x) + \alpha v_i(x) + w_i(x)) + h(x) t(x)]_T
\end{align*}
$$

In the WKEM Equation Derivation section, we know:

Substituting into the equation, we can eliminate the parts containing $\alpha, \beta$:

$$
\begin{align*}
[\sum_{i=0}^m & a_{A,i} u_i(x) \sum_{i=0}^m a_{B,i}v_i(x)]_T \\
= & \sum_{i=0}^{\ell} a_i \left[w_i(x) \right]_T + \sum_{i=\ell+1}^m [a_{C,i} w_i(x) + h(x) t(x)]_T
\end{align*}
$$

In the WKEM Equation Derivation section, we have already verified this equation holds, so this Proof will pass Groth16’s Verify algorithm and output 1.

From Groth16 Security to WKEM Security

Since this Proof is valid, according to the Soundness definition, the probability that a $w$ cannot be extracted from this proof such that $({a_i}_{i=0}^{\ell}, {a_i}_{i=\ell+1}^{m}) \in R$ is negligible. We let the WKEM extractor output the $w$ from the Groth16 extractor, and we get:

$$
\text{Pr}\left[
(\{a_i\}_{i=0}^{\ell}, \{a_i\}_{i=\ell+1}^{m}) \in R :
\begin{array}{r}
\{a_i\}_{i=0}^{\ell} \leftarrow \mathcal{A}(1^\lambda, R) \\
\{a_i\}_{i=\ell+1}^{m} \leftarrow \text{Ext}^{\mathcal{A}(\cdot, \cdot)}(R, \{a_i\}_{i=0}^{\ell})
\end{array}
\right] \\
= 1 - \text{negl}_{CKS}(\lambda) \geq \delta(\lambda)
$$

Therefore, our security satisfies the definition.

Conclusion

This research is based on the QAP design commonly used in zkSNARK. Since Groth16 was proposed, well-known projects like Circom have been able to help developers convert programs into QAP. Based on Groth16’s architecture, we designed a WKEM-WE scheme, enabling these existing tools to be used directly, which gives our scheme higher feasibility.

However, considering the development of quantum computers, and like Groth16, our scheme is not quantum-resistant. On the other hand, zkSNARK has had many quantum-resistant designs in recent years, so our research approach might be applicable to other schemes, thereby proposing quantum-resistant and practical Witness Encryption schemes.