Groth16を使った見証暗号の構築

翻訳注記: この記事は機械翻訳されたものです。専門用語や表現について不正確な部分がある可能性があります。

（トラウマ警告：本稿には大量の数学と暗号学が含まれます。）

見証暗号（Witness Encryption）は暗号化方式の一種で、NP 命題（Statement）を暗号化に使用し、対応する見証（Witness）で復号化するという特徴があります。Groth16 は古典的な zkSNARK 方式で、ある当事者が特定の NP 関係を満たす命題と見証のペアを知っていることを証明できます。Groth16 が構築する方式は回路充足可能性問題（Circuit satisfiability problem, CircuitSAT）に基づいており、この問題は NP 完全であるため、任意の NP 問題をこの問題に還元してから Groth16 で zkSNARK の証明者と検証者を構築できます。これに基づいて、我々は Groth16 を見証暗号に変換することを試み、つまり CircuitSAT に基づく見証暗号を構築することで、任意の NP 問題を暗号化・復号化に使用できるようにします。

本稿は私の修士論文「二次算術プログラムに適用可能な見証暗号方式」の抜粋と安全性証明の補正です。

中文版 | 日本語 | English

背景知識

構築方法を説明する前に、いくつかの背景知識を紹介します。自信のある方は直接構築セクションにお進みください。ここでは楕円曲線暗号学、双線形写像群などの詳細な数学的知識の紹介は省略します（延伸閱讀：楕円曲線ペアリングの探求）。Groth16 論文と同じ記法を使用し、$[a]_1\cdot[b]_2 = [c]_T$の形で群元素とペアリング計算を表現します。

見証暗号（Witness Encryption）

見証暗号はGarg らが 2013 年に提案しました。NP 言語 $\mathcal{L}$に対して、暗号化者は命題 $x$で暗号化でき、復号化者は見証 $w$で復号化します。ここで$(x, w) \in R_\mathcal{L}$です。例えば、数独のルールを使って関係を構築し、見証暗号を利用して暗号化システムを設計できます。このシステムでは数独の問題を使って暗号化し、答えを解いた人が復号化できます。

見証暗号は NP 問題に基づいて構築されるため、現実の検証問題を使って関係を構築できます。これに基づいて見証暗号方式を設計できれば、より自由に暗号化・復号化システムを設計できます。例えば、NFT をコンテンツの所有権として使用するアプリケーションシナリオでは、特定の NFT を持つ人のみがコンテンツを復号化できるようにしたいとします。その場合、NFT のコントラクトアドレス、Token ID を命題とし、ブロックチェーンの有効な状態と所有者の身元証明（署名など）を見証とすることで、我々の要求を満たすことができます。

見証鍵カプセル化機構（Witness Key Encapsulation Mechanism）

Key Encapsulation Mechanism (KEM)はハイブリッド暗号化の一般的な方法で、概念的には暗号化を鍵生成部分と対称暗号化部分に分けます。両側はまず異なる方法で同じ鍵を計算し、この鍵を対称暗号化で使用します。これは対称暗号化の効率が通常他の暗号化方式（非対称暗号化など）より高く、平文空間がすべての暗号化可能な文字列を含むためです。対照的に、非対称暗号化などの方法は通常限定された平文空間を使用し、平文を指定して暗号化するのは容易ではありません。逆に、アルゴリズム設計を通じて暗号化側と復号化側が同じ鍵を計算できるようにする方がより容易です。

近年、見証暗号の多くの設計が提案されており、本稿ではその中の一つの設計方式を使用します。その名前は見証鍵カプセル化機構 (WKEM)です。WKEM は最初に Gwangbae Choi と Serge Vaudenay によって提案されました。本研究でも同じ方式を使用し、WKEM を設計して対称暗号化方式と組み合わせて完全な見証暗号を構築します。

WKEM は二つのアルゴリズムで構成されます：$\text{Encap}, \text{Decap}$。（説明を簡単にするため、ここでは原論文と異なり、直接関係 $R$を使用します。）

$(\text{ct}, k) \leftarrow \text{Encap}(R, x)$：関係、命題を入力とし、暗号文$\text{ct}$と鍵$k$を出力。
$k \leftarrow \text{Decap}(R, \omega, \text{ct})$：関係、見証、暗号文$\text{ct}$を入力とし、鍵$k$を出力。

つまり、暗号化者は関係と命題を使ってまず鍵を生成でき、見証を持つ者は暗号文を使って同じ鍵を生成でき、これによって見証暗号の目標を達成します。

WKEM では、我々は二つの安全性質に注目します：正しさ（Correctness）と抽出可能性（Extractability）。正しさは、正しいアルゴリズムに従って計算すれば、有効な関係、命題、見証に対して同じ鍵を出力できるべきことを意味します。概略的に抽出可能性を言うと、正しい鍵を出力できる復号化者に対して、我々は彼が正しい見証を持っていると考えます。

本研究では、以下の定義を使用します：

WKEM の抽出可能性：任意の非一様有状態確率多項式時間攻撃者（Non-uniform stateful probabilistic polynomial time adversary）と任意の関係に対して、非一様確率多項式時間抽出器（Non-uniform probabilistic polynomial time extractor）が存在し、ある無視できる関数$\epsilon(\lambda)$に対して

$$
\text{Pr}[\text{Expt}^\text{CPA}_{\text{WKEM},\mathcal{A}}(1^\lambda, R) = 1] \geq \frac{1}{2} + \epsilon(\lambda)
$$

が成り立つなら、ある無視できる関数$\delta(\lambda)$に対して、次の式が成立します：

$$
\text{Pr}\left[
(x, w) \in R :
\begin{array}{r}
x \leftarrow \mathcal{A}(1^\lambda, R) \\
w \leftarrow \text{Ext}^{\mathcal{A}(\cdot, \cdot)}(R, x)
\end{array}
\right] \geq \delta(\lambda)
$$

ここで第二の確率は$\mathcal{A}$と抽出器$\text{Ext}$のランダム性に関するサンプリングです。

$\text{Expt}^\text{CPA}_{\text{WKEM},\mathcal{A}}(1^\lambda, R)$の定義は：

$$
\begin{array}{l}
\mathbf{Expt}_{\mathsf{WKEM}, \mathcal{A}}^{\mathsf{CPA}}(1^\lambda, R) \\
\hline
x \leftarrow \mathcal{A}(1^\lambda, R) \\
b \overset{$}{\leftarrow} {0, 1} \\
(ct, k_0) \leftarrow \mathsf{Encap}(R, x) \\
k_1 \overset{$}{\leftarrow} \mathcal{K} \\
b’ \leftarrow \mathcal{A}(ct, k_b) \\
\mathbf{return} \begin{cases}
1 & \text{if } b’ = b \\
0 & \text{otherwise}
\end{cases}
\end{array}
$$

この実験では、攻撃者に関係を提供し、攻撃者が任意の命題を生成し、我々がこの命題を使って暗号化し、生成された鍵$k_0$とランダムに選択された$k_1$をランダムに攻撃者に送信し、攻撃者は得られた鍵が真の鍵かランダムに選択された鍵かを判定する必要があります。したがって、この定義の意味は：攻撃者の正答率がランダム推測よりも高い場合、抽出器が見証を得て、命題と見証が関係を満たす確率が無視できない、ということです。

この記事では、攻撃者と抽出器を非一様に修正しました。これは我々の安全性が Groth16 の安全性証明に適合するためであり、他の WKEM 方式（および原論文）とは異なります。後続の証明では我々は Groth16 の Soundness 証明と組み合わせて証明を完成させます。本稿では一様攻撃者と抽出器を維持する他の証明方式が存在すると考えますが、本研究では探究しません。

zkSNARK

本研究は最終的に zkSNARK 方式である Groth16 から見証暗号を構築したいため、zkSNARK のいくつかの性質を使用します。そのため簡単に紹介します。

zkSNARK は零知識証明システムの一種で、Zero-knowledge、Succinct、Non-interactive、そして Argument of Knowledge という特徴を持ちます。Argument of Knowledge は、このシステムが証明者に論拠（Argument）を提出させ、検証者に彼がある知識を知っていることを納得させることを意味します。（Proof of Knowledge は証明があれば必ず知識があることを要求するのに対し、Argument of Knowledge は証明者が極小確率の状況で論拠を計算することを許可し、そのためより設計しやすいです。）Non-interactive は証明者が検証者に一度だけ証明を与えればよいことを意味します。（対照的なのは Interactive Proof System で、証明者が検証者の挑戦を受けて応答することを要求する場合があります。）Succinct は証明が直接答えを与えるよりも効率的であることを要求します。なぜなら最も直接的な知識証明は知識そのものだからです。Zero-knowledge は検証者が知識そのものに関する性質を得ることができず、証明者が知識を持っているかどうかのみを知ることができることを意味します。

zkSNARK は四つのアルゴリズムで構成されます：Setup、Prove、Verify、Simulator。Setup は関係に対してシステム設定を生成し、公開情報とトラップドア（Trapdoor）を含み、トラップドアは Simulator で使用されます。Prove は関係、公開情報、命題、見証を受け取って証明を出力し、Verify は関係、公開情報、命題、証明を受け取って成立するかどうかを判定します。Simulator は Zero-knowledge 性質を証明するために使用され、関係、命題、トラップドアを使って模擬証明を生成します。紙面の都合上、詳細は説明しません。

本研究で主に必要な性質は「証明があれば必ず知識がある」ことのみで、学術的専門用語では「Soundness」です。そのため具体的定義を説明します：

Soundness： すべての非一様多項式時間攻撃者$\mathcal{A}$に対して、非一様多項式時間抽出器（Extractor）$\text{Ext}$が存在し（この抽出器はすべての$\mathcal{A}$の状態を使用可能）、以下の関係を満たします：

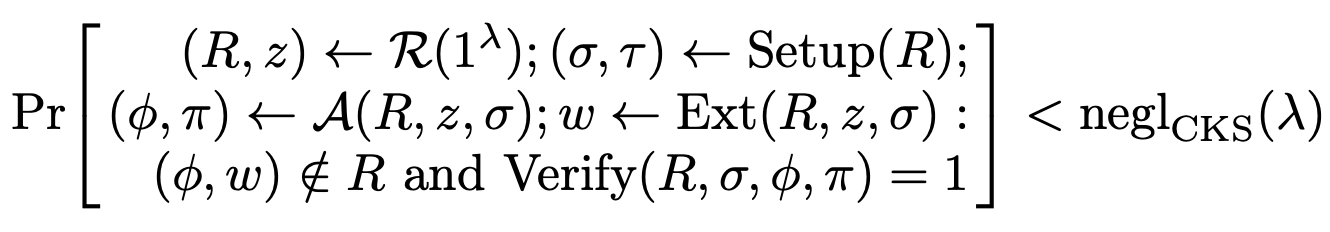
ここで$\text{negl}_\text{CKS}(\lambda)$は無視できる関数、$R$は関係で、ここでは Generator $\mathcal{R}$で表現、$\sigma, \tau$はシステム構築時に生成される情報、$\phi$は命題、$\pi$は Proof、$\omega$は見証です。

この定義は一見理解しにくいかもしれませんが、簡単に言うと：攻撃者が有効な命題と Proof のペアを生成できる場合、この攻撃者の内部状態と公開情報を利用して見証を生成し、命題と関係に属する抽出器が存在することを意味します。（つまり Proof があれば見証がある。）

Groth16

Groth16 は代表的な zkSNARK 方式で、以下の形式の二次算術プログラム（Quadratic Arithmetic Program, QAP）関係を受け入れます：

$$
R = (p, \mathbb{G}_1, \mathbb{G}_2, \mathbb{G}_T, e, g, h, \ell, \{ u_i(X), v_i(X), w_i(X) \}^m_{i=0}, t(X))
$$

この関係は双線形写像群と命題と見証の言語 $(a_1,…, a_\ell) \in \mathbb{Z}_p^\ell$、$(a_{\ell+1},…a_m) \in \mathbb{Z}_p^{m-\ell}$を定義し、$a_0 = 1$を満たします

$$
\sum_{i=0}^{m}a_iv_i(X) \cdot \sum_{i=0}^{m}a_iv_i(X) = \sum_{i=0}^{m}a_iw_i(X) + h(X)t(X)
$$

ここで$h(X)$はある次数$n−2$の商多項式、$n$は$t(X)$の次数です。

Groth16 のアルゴリズム定義は以下の通りです：

Algebraic Group Model (AGM)

Algebraic group model (AGM)は安全性分析モデルです。このモデルでは、アルゴリズムは代数的（Algebraic）です。これはアルゴリズムが群上で代数演算を実行できるが、係数組み合わせを提供しなければならないことを意味します。例えば$[a]_1, [b]_1$を入力とするアルゴリズムは、$2[a]_1, [a + b]_1$を出力できます。これらは係数組み合わせ（$(2, 0), (1, 1)$）で表現できるからです。しかし$[ab]_1$の係数を出力できないため、この演算は実行できません。

我々はMatteo Campanelli らが提案した定義を使用します：

構築

本研究はFleischhaker らの研究と同じ WKEM-WE 構造と WKEM の表現法を使用します。その研究では WKEM を使って見証暗号を構築する方法を説明し、関連する安全性を証明しました。そのため我々はここでは WKEM の構築方法の説明に集中します。

WKEM for QAP

我々は QAP に基づいて WKEM を定義します。Groth16 と同じ QAP 形式を使用します。$\text{Encap}, \text{Decap}$アルゴリズムを以下のように定義します：

ここで$H$は Random Oracle で、$\mathbb{G}_T$要素を Key space 中の要素$k$に変換します。

概観すると、暗号化者は$\sigma$を復号化を試みる者に渡し、復号化者は$s$を計算する際に$\{[r^2w_i(x)]_1\}^\ell_{i=0}$が必要です。$r$は離散対数問題により他の要素から取り出すことができないため、復号化者は他の方法で計算する必要があります。（$\sigma$中で直接関連情報を含むのは$i$が$\ell+1$から$m$の間に限られることに注意。）この他の方法が前述の関係式です。この関係式を使用するには、復号化者は命題と見証が必要です。

安全性証明

前述したように WKEM は二つの安全性質に注目します：正しさと抽出可能性。正しさはアルゴリズムの検証によって簡単に確認できるため、本稿では詳しく説明しません。次は抽出可能性の証明に集中します。

$\mathcal{A}$を非一様確率多項式時間攻撃者とし、

$$
\text{Pr}[\text{Expt}^\text{CPA}_{\text{WKEM},\mathcal{A}}(1^\lambda, R) = 1] \geq \frac{1}{2} + \epsilon(\lambda)
$$

を満たすとします。我々は抽出器を構築できます。この抽出器は Groth16 の Setup アルゴリズムを実行し、$\sigma_\text{Groth16}$を取得します。次に、この抽出器は修正された$\text{Encap}$アルゴリズムを実行し、$\sigma_\text{Groth16}$中の

$$
([\alpha]_1, [\beta]_1, [\beta]_2, \{[x^i]_1\}_{i=0}^{n-1}, \{[x^i]_2\}_{i=0}^{n-1})
$$

を使用します（Groth16 Setup アルゴリズムも同様にランダム選択するため、この修正は原アルゴリズムを完全に模擬します）。

ベクトルの抽出

抽出器は$s$を保存し（以下$\hat{s}$を使用、攻撃者のものと区別するため）、$(\text{ct}, k_0)$を計算し、ランダムに$k_1 \leftarrow K$（$K$は Key space）と一つの Bit $b \leftarrow \{0, 1\}$を選択します。次に抽出器は空のリスト$\Gamma$を作成し、$\mathcal{A}$が Random Oracle（$H$）を使用する際、この抽出器はその Random Oracle を模擬し、入力値に応じて以下の行動を取ります：$s \neq \hat{s}$の場合、抽出器は$(s, k’)$が$\Gamma$に存在するかチェックし、存在すれば$k’$を返し、そうでなければランダムに$k’$を選択後$\Gamma$に保存して返します；$s = \hat{s}$の場合、$\mathcal{A}$を中断して$k$を返します。

この攻撃者は AGM 下で実行されるため、攻撃者の入力を考慮します：

$$
[\mathcal{X}]_1 = ([\alpha]_1, \{[ru_i(x)]_1\}_{i=0}^m) \\
[\mathcal{Y}]_2 = ([\beta]_2, \{[rv_i(x)]_2\}_{i=0}^m) \\
[\mathcal{Z}]_T = ( \{ [r\beta u_i(x) + r\alpha v_i(x) + r^2w_i(x)]_T \}^m_{i=\ell+1}, \{ [r^2 x^i t(x)]_T \}^{n-2}_{i=0})
$$

ここで$[\mathcal{Z}]_T$は以下の計算で得られます：

$$
[r\beta u_i(x) + r\alpha v_i(x) + r^2w_i(x)]_T = [\frac{r\beta u_i(x) + r\alpha v_i(x) + r^2w_i(x)}{\delta}]_1 \cdot [\delta]_2 \\
[r^2 x^i t(x)]_T = [\frac{r^2 x^i t(x)}{\delta}]_1 \cdot [\delta]_2
$$

攻撃者はまたベクトルを出力します：

$$
((\mathcal{A}_{i,j})_{i\in[m],j\in[m]}, (\mathcal{B}_{i})_{i\in[m-\ell-1+n-2]})
$$

我々は$\mathcal{A}_{i.j}, \mathcal{B}_{i}$の対応関係に注目します。

$\mathcal{A}_{0,0}$は$[\alpha]_1 \cdot [\beta]_2$の係数に相当し、1 に固定、${\mathcal{A}_{0,i}}_{i=0}^m$は$B$計算中の$\{a_i\}_{i=0}^m$に相当（後で$\{a_{B,i}\}_{i=0}^m$と記述）、$\{\mathcal{A}_{i,0}\}_{i=0}^m$は$A$計算中の$\{a_i\}_{i=0}^m$に相当（後で$\{a_{A,i}\}_{i=0}^m$と記述）、その他の部分は$a_{A,i}a_{B,i}$で、後続で使用しないためスキップします。

$\{\mathcal{B}_{i}\}_{i=0}^{m-\ell-1}$は$C$計算中の$\{a_i\}_{i=\ell+1}^m$に相当（後で$\{a_{C,i}\}_{i=\ell+1}^m$と記述）。$\{\mathcal{B}_{i}\}_{i=m-\ell}^{m-\ell-1+n-2}$は$h(x)$の係数に相当します。

WKEM 等式導出

Encap アルゴリズムの$s$と攻撃者の$s$が等しいことから、以下の等式を得ることができます：

$$
\begin{align*}
s = &[\alpha]_1 \cdot [\beta]_2 + \sum^\ell_{i=0} a_i[r\beta u_i(x) + r\alpha v_i(x) + r^2w_i(x)]_1 \cdot [1]_2 \\
= &([\alpha]_1 + \sum^{m}_{i=0}a_{A,i} [ru_i(x)]_1) \cdot ([\beta]_2 + \sum^{m}_{i=0}a_{B,i} [rv_i(x)]_2) \\
& - (\sum^{m}_{i=\ell+1}a_{C,i}[\frac{r\beta u_i(x) + r\alpha v_i(x)+r^2w_i(x)}{\delta}]_1 + [\frac{r^2h(x)t(x)}{\delta}]_1) \cdot [\delta]_2
\end{align*}
$$

簡略化すると：

$$
\begin{align*}
\sum^\ell_{i=0} & a_i[r\beta u_i(x) + r\alpha v_i(x) + r^2w_i(x)]_1 \cdot [1]_2 \\
= \sum^{m}_{i=0} & a_{A,i} [ru_i(x)]_1 \cdot [\beta]_2 + \sum^{m}_{i=0} a_{B,i} [\alpha]_1 \cdot [rv_i(x)]_2 \\
& + (\sum^{m}_{i=0}a_{A,i} [ru_i(x)]_1) \cdot (\sum^{m}_{i=0}a_{B,i} [rv_i(x)]_2) \\
& - (\sum^{m}_{i=\ell+1}a_{C,i}[\frac{r\beta u_i(x) + r\alpha v_i(x)+r^2w_i(x)}{\delta}]_1 + [\frac{r^2h(x)t(x)}{\delta}]_1) \cdot [\delta]_2
\end{align*}
$$

両辺を$\mathbb{G}_T$の値で計算します：

$$
\begin{align*}
\sum^\ell_{i=0} & a_i[r\beta u_i(x) + r\alpha v_i(x) + r^2w_i(x)]_T \\
= \sum^{m}_{i=0} & a_{A,i} [r\beta u_i(x)]_T + \sum^{m}_{i=0} a_{B,i} [r\alpha v_i(x)]_T \\
& + [\sum^{m}_{i=0}a_{A,i} ru_i(x) \sum^{m}_{i=0}a_{B,i} rv_i(x)]_T \\
& - (\sum^{m}_{i=\ell+1}a_{C,i}[r\beta u_i(x) + r\alpha v_i(x)+r^2w_i(x)]_T + [r^2h(x)t(x)]_T)
\end{align*}
$$

等式を整理し、$w(x)$を含む項を右辺に、含まない項を左辺に移動し、両辺を$r^2$で割ります：

$$
\begin{align*}
[\sum^{m}_{i=0} & a_{A,i} u_i(x) \sum^{m}_{i=0}a_{B,i} v_i(x)]_T \\
& + \sum^{m}_{i=0} a_{A,i} [\frac{\beta u_i(x)}{r}]_T + \sum^{m}_{i=0} a_{B,i} [\frac{\alpha v_i(x)}{r}]_2 \\
= \sum^\ell_{i=0} & a_i[\frac{\beta u_i(x)}{r} + \frac{\alpha v_i(x)}{r} + w_i(x)]_T \\
& + (\sum^{m}_{i=\ell+1}a_{C,i}[\frac{\beta u_i(x)}{r} + \frac{\alpha v_i(x)}{r}+w_i(x)]_T + [h(x)t(x)]_T)
\end{align*}
$$

$\frac{\alpha}{r}, \frac{\beta}{r}$を観察すると、この値は 0 に等しくなく、その係数は他の項と無関係であることが分かります。そのため以下を得ることができます：

$$
\sum^{m}_{i=0} a_{A,i} u_i(x) - \sum^{\ell}_{i=0} a_{i} u_i(x) - \sum^{m}_{i=\ell+1} a_{C,i} u_i(x) = 0 \\
\sum^{m}_{i=0} a_{B,i} v_i(x) - \sum^{\ell}_{i=0} a_{i} v_i(x) - \sum^{m}_{i=\ell+1} a_{C,i} v_i(x) = 0
$$

前のステップの式をさらに整理すると：

$$
\begin{align*}
[\sum^{m}_{i=0} & a_{A,i} u_i(x) \sum^{m}_{i=0}a_{B,i} v_i(x)]_T \\
& = \sum^\ell_{i=0} a_i[w_i(x)]_T + (\sum^{m}_{i=\ell+1}a_{C,i}[w_i(x)]_T + [h(x)t(x)]_T)
\end{align*}
$$

抽出器による Groth16 証明の構築

抽出器が攻撃者からこれらの係数を取得した後、Groth16 Proof $[A’]_1, [B’]_2, [C’]_1$を構築できます

$$
\begin{align*}
A’ &= \alpha + \sum_{i=0}^m a_{A,i} u_i(x) + r’ \delta’ \\
B’ &= \beta + \sum_{i=0}^m a_{B,i} v_i(x) + s’ \delta’ \\
C’ &= \sum_{i=\ell+1}^m \frac{ a_{C,i} (\beta u_i(x) + \alpha v_i(x) + w_i(x)) + h(x) t(x)}{\delta’} + s’A + r’B - r’s’\delta’
\end{align*}
$$

ここで$r’, s’, \delta’$は$\sigma_\text{Groth16}$から来ています。この三つの要素を Groth16 の Verify アルゴリズムに代入します：

$$
\begin{align*}
[A’]_1 \cdot &[B’]_2 = \\
& [\alpha]_1 \cdot [\beta]_2 + \sum_{i=0}^{\ell} a_i \left[ \frac{\beta u_i(x) + \alpha v_i(x) + w_i(x)}{\gamma} \right]_1 \cdot [\gamma]_2 + [C’]_1 \cdot [\delta’]_2
\end{align*}
$$

展開すると：（式が長くなるのを避けるため、最後の行はここでは展開しません。簡単に言うと、その行は$A’, B’$中の$r’\delta’, s’\delta’$部分を消去します。）

$$
\begin{align*}
([\alpha]_1 + & \sum_{i=0}^m a_{A,i} [u_i(x)]_1 + r [\delta’]_1) \cdot ([\beta]_2 + \sum_{i=0}^m a_{B,i} [v_i(x)]_2 + s [\delta’]_2) = \\
[\alpha]_1 &\cdot [\beta]_2 + \sum_{i=0}^{\ell} a_i \left[ \frac{\beta u_i(x) + \alpha v_i(x) + w_i(x)}{\gamma} \right]_1 \cdot [\gamma]_2 \\
& + (\sum_{i=\ell+1}^m [\frac{ a_{C,i} (\beta u_i(x) + \alpha v_i(x) + w_i(x)) + h(x) t(x)}{\delta}]_1) \cdot [\delta’]_2 \\
& + (s’[A]_1 + r’[B]_1 - [r’s’\delta’]_1) \cdot [\delta’]_2
\end{align*}
$$

左右の等しい値を消去すると：

$$
\begin{align*}
(\sum_{i=0}^m a_{A,i} & [u_i(x)]_1) \cdot (\sum_{i=0}^m a_{B,i}[v_i(x)]_2) \\
& + \sum_{i=0}^m a_{B,i} [\alpha]_1 \cdot [v_i(x)]_2 + \sum_{i=0}^m a_{A,i} [u_i(x)]_1 \cdot [\beta]_2 = \\
\sum_{i=0}^{\ell} a_i & \left[ \frac{\beta u_i(x) + \alpha v_i(x) + w_i(x)}{\gamma} \right]_1 \cdot [\gamma]_2 \\
& + (\sum_{i=\ell+1}^m [\frac{ a_{C,i} (\beta u_i(x) + \alpha v_i(x) + w_i(x)) + h(x) t(x)}{\delta}]_1) \cdot [\delta’]_2
\end{align*}
$$

両辺を$\mathbb{G}_T$の値で計算します：

$$
\begin{align*}
[\sum_{i=0}^m & a_{A,i} u_i(x) \sum_{i=0}^m a_{B,i}v_i(x)]_T + \sum_{i=0}^m a_{B,i} [\alpha v_i(x)]_T + \sum_{i=0}^m a_{A,i} [\beta u_i(x)]_T \\
= & \sum_{i=0}^{\ell} a_i \left[ \beta u_i(x) + \alpha v_i(x) + w_i(x) \right]_T \\
& + \sum_{i=\ell+1}^m [a_{C,i} (\beta u_i(x) + \alpha v_i(x) + w_i(x)) + h(x) t(x)]_T
\end{align*}
$$

WKEM 等式導出セクションで、我々は次のことを知っています：

式に代入すると、$\alpha, \beta$を含む部分を消去できます：

$$
\begin{align*}
[\sum_{i=0}^m & a_{A,i} u_i(x) \sum_{i=0}^m a_{B,i}v_i(x)]_T \\
= & \sum_{i=0}^{\ell} a_i \left[w_i(x) \right]_T + \sum_{i=\ell+1}^m [a_{C,i} w_i(x) + h(x) t(x)]_T
\end{align*}
$$

WKEM 等式導出セクションで、我々はすでにこの等式が成立することを検証したため、この Proof は Groth16 の Verify アルゴリズムを通過し、1 を出力します。

Groth16 安全性から WKEM 安全性へ

この Proof が有効であるため、Soundness 定義により、この証明から$({a_i}_{i=0}^{\ell}, {a_i}_{i=\ell+1}^{m}) \in R$を満たす$w$を抽出できない確率は無視できます。WKEM の抽出器に Groth16 抽出器の$w$を出力させると：

$$
\text{Pr}\left[
(\{a_i\}_{i=0}^{\ell}, \{a_i\}_{i=\ell+1}^{m}) \in R :
\begin{array}{r}
\{a_i\}_{i=0}^{\ell} \leftarrow \mathcal{A}(1^\lambda, R) \\
\{a_i\}_{i=\ell+1}^{m} \leftarrow \text{Ext}^{\mathcal{A}(\cdot, \cdot)}(R, \{a_i\}_{i=0}^{\ell})
\end{array}
\right] \\
= 1 - \text{negl}_{CKS}(\lambda) \geq \delta(\lambda)
$$

したがって我々の安全性は定義を満たします。

結論

本研究は zkSNARK でよく使用される QAP 設計に基づいており、Groth16 が提案されて以来、Circom などの著名なプロジェクトが開発者がプログラムを QAP に変換するのを支援できるようになりました。我々は Groth16 の構造に基づいて WKEM-WE 方式を設計することで、これらの既存ツールを直接使用できるようになり、我々の方式の実現可能性を高めています。

しかし量子コンピュータの発展を考慮すると、Groth16 と同様に、我々の方式は量子耐性ではありません。一方で、zkSNARK は近年多くの量子耐性設計も提案されているため、我々の研究手法は他の方式にも適用でき、量子耐性で実現可能な見証暗号方式を提案することができるかもしれません。