用 Groth16 做出一個 Witness Encryption

（創傷警告：本文具有許多數學與密碼學。）

Witness Encryption 是一種加密方式的類型，其特點在於用於加密的是一個 NP Statement，並使用對應的 Witness 解密。Groth16 是一個經典的 zkSNARK 方案，允許一方證明某對 Statement 與 Witness 滿足特定 NP 關係。Groth16 建立的方案基於電路可滿足性問題（Circuit satisfiability problem，CircuitSAT），而該問題是 NP 完全，因此任意 NP 問題都可以規約到此問題後透過 Groth16 建立 zkSNARK 的證明者與驗證者。基於此，我們可以試著將 Groth16 轉換成一個 Witness Encryption，也就是構造一個基於 CircuitSAT 的 Witness Encryption，從而使我們可以用任意 NP 問題進行加解密。

本文是對我自己的碩士論文《適用於二次算術程式的見證加密方案》的節錄與安全性證明的補正。

背景知識

在開始說明建構方式之前，我將介紹一些背景知識。對自己有信心的人可直接前往 建構 段落。我們這裡將省略介紹橢圓曲線密碼學、雙線性映射群等細節數學知識（延伸閱讀：探索橢圓曲線對）。我們將使用與 Groth16 論文相同的寫法，以 $[a]_1\cdot[b]_2 = [c]_T$ 的方式表達群元素與 Pairing 計算。

Witness Encryption

Witness Encryption 是 Garg 等人於 2013 年提出。對於一個 NP Language $\mathcal{L}$，加密者可以透過一個 Statement $x$ 進行加密，解密者通過一個 Witness $w$，其中 $(x, w) \in R_\mathcal{L}$，進行解密。例如我們可以利用一個數獨的規則構建一個 Relation，並使用 Witness Encryption 制定一個加密系統，這個系統使用數獨的題目進行加密，而解出答案的人便可解密。

由於 Witness Encryption 是基於 NP 問題建構，我們可以用現實的驗證問題構建一個 Relation，而如果能據此制定出 Witness Encryption 方案，我們就可以更自由的設計加解密系統。例如在 NFT 作為內容所有權的應用場景中，我們希望只有持有特定 NFT 的人可以解密內容。那我們可以將 NFT 的合約地址、Token ID 作為 Statement，將區塊鏈的有效狀態和持有者的身分證明（如簽章）作為 Witness，就可以達成我們的需求。

Witness Key Encapsulation Mechanism

Key Encapsulation Mechanism (KEM) 是混合加密的常見方法，概念上是將加密分為金鑰產生部分與對稱式加密部分。兩邊首先透過不同方式計算出相同密鑰，使用此密鑰於對稱式加密中。這是因為對稱式加密的效率通常高於其他加密方式（如非對稱式加密），且明文空間包含所有可加密的字串。相較之下，非對稱式加密等方法通常使用有限的明文空間，指定明文並進行加密並不容易。相反的，透過演算法設計使加密與解密方能夠計算出相同金鑰要更為容易。

近年，Witness Encryption 有許多設計被提出，而本文使用了其中一種設計方式，其名為 Witness Key Encapsulation Mechanism (WKEM)。WKEM 首先由 Gwangbae Choi 與 Serge Vaudenay 提出。在本研究中也使用相同方式，設計一個 WKEM 並配合一個對稱式加密方案來建構完整的 Witness Encryption。

一個 WKEM 由兩個演算法組成：$\text{Encap}, \text{Decap}$。（為了簡化說明，在這裡與原論文不同，將直接使用 Relation $R$。）

• $(\text{ct}, k) \leftarrow \text{Encap}(R, x)$：輸入 Relation、Statement，輸出密文 $\text{ct}$ 與密鑰 $k$。
• $k \leftarrow \text{Decap}(R, \omega, \text{ct})$：輸入 Relation、Witness、密文 $\text{ct}$，輸出密鑰 $k$。

也就是說，加密者可以使用 Relation 和 Statement 首先產生出密鑰，而具備 Witness 者則可以使用密文產生出相同密鑰，藉此達到 Witness Encryption 的目標。

而在 WKEM 中，我們關注兩個安全性質：正確性（Correctness）與可提取性（Extractability）。正確性意味著如果按照正確的演算法計算，則對有效的 Relation、Statement、Witness，應該要能輸出相同密鑰。而概略地說可提取性，對於能夠正確輸出密鑰的解密者，我們認為他具備正確的 Witness。

在本研究中，我們使用的定義如下：

WKEM 的可提取性：如果對任意非均勻有狀態的機率多項式時間攻擊者（Non-uniform stateful probabilistic polynomial time adversary）與任意 Relation，均存在一個非均勻機率多項式時間提取器（Non-uniform probabilistic polynomial time extractor），對於某個可忽略函數 $\epsilon(\lambda)$ 滿足

$$
\text{Pr}[\text{Expt}^\text{CPA}_{\text{WKEM},\mathcal{A}}(1^\lambda, R) = 1] \geq \frac{1}{2} + \epsilon(\lambda)
$$

則對於某個可忽略函數 $\delta(\lambda)$，此式子成立：

$$
\text{Pr}\left[
(x, w) \in R :
\begin{array}{r}
x \leftarrow \mathcal{A}(1^\lambda, R) \\
w \leftarrow \text{Ext}^{\mathcal{A}(\cdot, \cdot)}(R, x)
\end{array}
\right] \geq \delta(\lambda)
$$

。其中第二個機率是在 $\mathcal{A}$ 與提取器 $\text{Ext}$ 的隨機性上取樣。

$\text{Expt}^\text{CPA}_{\text{WKEM},\mathcal{A}}(1^\lambda, R)$ 定義為：

$$
\begin{array}{l}
\mathbf{Expt}_{\mathsf{WKEM}, \mathcal{A}}^{\mathsf{CPA}}(1^\lambda, R) \\
\hline
x \leftarrow \mathcal{A}(1^\lambda, R) \\
b \overset{$}{\leftarrow} {0, 1} \\
(ct, k_0) \leftarrow \mathsf{Encap}(R, x) \\
k_1 \overset{$}{\leftarrow} \mathcal{K} \\
b’ \leftarrow \mathcal{A}(ct, k_b) \\
\mathbf{return} \begin{cases}
1 & \text{if } b’ = b \\
0 & \text{otherwise}
\end{cases}
\end{array}
$$

在此實驗中，我們提供 Relation 給攻擊者，攻擊者產生任意 Statement，我們再使用此 Statement 進行加密，並將產生的密鑰 $k_0$ 與隨機選取的 $k_1$ 隨機發送給攻擊者，攻擊者需要判定得到的密鑰是真實的密鑰或隨機選取的密鑰。因此定義的白話意思便是：如果存在一個攻擊者的正確機率比隨機猜測還要高，那提取器得到 Witness，且 Statement 與 Witness 滿足 Relation 的機率就為不可忽略。

在這篇文章中，我們修改攻擊者與提取器為非均勻的，這是為了使我們的安全性可以切合 Groth16 的安全性證明，這與其他 WKEM 方案（和原始論文）不同。後續證明中我們將與 Groth16 的 Soundness 證明結合來完成我們的證明，本文認為存在其他證明方式可維持均勻攻擊者與提取器，但本研究將不探究。

zkSNARK

由於本研究最後想從一個 zkSNARK 方案：Groth16，建構出一個 Witness Encryption，我們會運用到一些 zkSNARK 的性質，因此簡單介紹如下。

zkSNARK 是一種零知識證明系統類型，特徵包含 Zero-knowledge、Succinct、Non-interactive，並是一種 Argument of Knowledge。Argument of Knowledge 意味著這個系統使證明者可以提出一個論據（Argument），說服驗證者他知道某個知識。（相比於 Proof of Knowledge，要求有證明必然有知識，Arugment of Knowledge 允許證明者在極小機率的狀況下算出一個論據，也因此更容易設計。）Non-interactive 讓證明者只需要給驗證者一次證明就好。（與之相對的是 Interactive Proof System，可能要求證明者接受驗證者的挑戰並回覆。）Succinct 則要求證明要比直接給答案更有效率，畢竟最直接的知識證明就是知識本身。Zero-knowledge 則是讓驗證者無法得知知識本身相關的性質，而只唯獨知道證明者是否具備知識。

一個 zkSNARK 由四個演算法組成：Setup、Prove、Verify、Simulator。Setup 對一個 Relation 產生一個系統設置，包含公開資訊與陷門（Trapdoor），陷門在 Simulator 中被使用。Prove 接受 Relation、公開資訊、Statement、Witness 並輸出證明，Verify 則接收 Relation、公開資訊、Statement、證明並判斷是否成立。Simulator 是用於證明零知識性質，使用 Relation、Statement、陷門來產生模擬的證明。由於篇幅因素將不說明細節。

在本研究中，我們主要需要的性質只有「有證明必然有知識」，學術的專有名詞是「Soundness」。因此在此我將說明具體定義：

Soundness： 對於所有非均勻多項式時間攻擊者 $\mathcal{A}$，存在一個非均勻多項式時間提取器（Extractor）$\text{Ext}$（該提取器可以使用所有 $\mathcal{A}$ 的狀態），滿足以下關係：

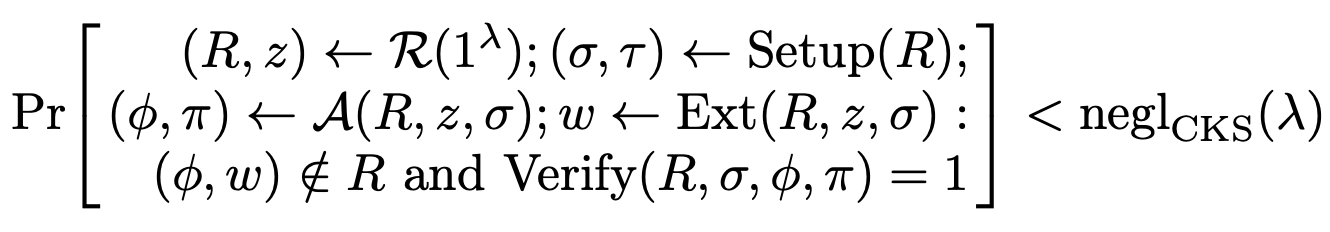
其中 $\text{negl}_\text{CKS}(\lambda)$ 是可忽略的函數，$R$ 是 Relation，這邊使用一個 Generator $\mathcal{R}$ 表示，$\sigma, \tau$ 是系統建立時產生的資訊，$\phi$ 是 Statement、$\pi$ 是 Proof，$\omega$ 是 Witness。

這邊定義可能乍看不容易理解，但簡單來說：如果攻擊者有辦法產生出一組有效的 Statement 和 Proof，意味著存在一個提取器可以利用這個攻擊者的內部狀態和公開資訊來產生 Witness，並且與 Statement 屬於 Relation。（所以有 Proof 意味著有 Witness。）

Groth16

Groth16 是一個具代表性的 zkSNARK 方案，該方案接受滿足以下格式的二次算數程式（Quadratic Arthimetic Program，QAP）Relation：

$$
R = (p, \mathbb{G}_1, \mathbb{G}_2, \mathbb{G}_T, e, g, h, \ell, \{ u_i(X), v_i(X), w_i(X) \}^m_{i=0}, t(X))
$$

這個 Relation 定義一個雙線性映射群和 Statement 與 Witeness 的 Language $(a_1,…, a_\ell) \in \mathbb{Z}_p^\ell$、$(a_{\ell+1},…a_m) \in \mathbb{Z}_p^{m-\ell}$，滿足 $a_0 = 1$

$$
\sum_{i=0}^{m}a_iv_i(X) \cdot \sum_{i=0}^{m}a_iv_i(X) = \sum_{i=0}^{m}a_iw_i(X) + h(X)t(X)
$$

其中 $h(X)$ 是某個次數為 $n−2$ 的商多項式，$n$ 是 $t(X)$ 的次數。

Groth16 的演算法定義如下：

Algebraic Group Model (AGM)

Algebraic group model (AGM) 是一個安全性分析模型。在這個模型中，演算法是代數的（Algebraic）。這意味著演算法可以在群上進行代數運算，但必須提供係數組合。例如輸入 $[a]_1, [b]_1$ 的演算法，他可以輸出 $2[a]_1, [a + b]_1$，因為這些可以被表達成係數組合（$(2, 0), (1, 1)$），但因為他無法輸出 $[ab]_1$ 的係數，因此無法進行這個運算。

我們使用 Matteo Campanelli 等人 提出的定義：

建構

本研究使用與 Fleischhacker 等人的研究 相同的 WKEM-WE 構造與 WKEM 的表示法。在該研究中說明了如何使用 WKEM 建立 Witness Encryption，並證明相關的安全性。因此我們在此將專注於說明如何建構 WKEM。

WKEM for QAP

我們將基於 QAP 定義一個 WKEM，我們使用與 Groth16 相同的 QAP 格式。我們定義 $\text{Encap}, \text{Decap}$ 演算法如下：

其中 $H$ 是一個 Random Oracle，將 $\mathbb{G}_T$ 元素轉換成一個 Key space 中的元素 $k$。

概觀而言，加密者將會把 $\sigma$ 傳遞給試圖解密者，解密者在計算 $s$ 上，需要的是 $\{[r^2w_i(x)]_1\}^\ell_{i=0}$。由於 $r$ 受限於離散對數問題，無法自其他元素中取出，因此解密者將需要其他方式計算。（注意到在 $\sigma$ 中，直接包含相關資訊的只限於 $i$ 在 $\ell+1$ 到 $m$ 之間。）這個其他方式就是前面提到的關係式。而若要使用此關係式，解密者需要 Statement 與 Witness。

安全性證明

前面提到 WKEM 關注兩個安全性質：正確性與可提取性。由於正確性可以簡單地透過檢驗演算法確認，本文將不展開說明。接下來將專注於證明可提取性。

使 $\mathcal{A}$ 是一個非均勻機率多項式時間攻擊者，滿足

$$
\text{Pr}[\text{Expt}^\text{CPA}_{\text{WKEM},\mathcal{A}}(1^\lambda, R) = 1] \geq \frac{1}{2} + \epsilon(\lambda)
$$

我們可以建構一個提取器。該提取器執行 Groth16 的 Setup 演算法，取得 $\sigma_\text{Groth16}$。接著，該提取器執行修改過的 $\text{Encap}$ 演算法，使用 $\sigma_\text{Groth16}$ 中的

$$
([\alpha]_1, [\beta]_1, [\beta]_2, \{[x^i]_1\}_{i=0}^{n-1}, \{[x^i]_2\}_{i=0}^{n-1})
$$

（由於 Groth16 Setup 演算法同樣是隨機選取，因此此修改完全模擬原始演算法）。

取出向量

提取器保存 $s$（以下使用 $\hat{s}$，以便與攻擊者的區分），計算出 $(\text{ct}, k_0)$，並隨機選取一把 $k_1 \leftarrow K$（$K$ 為 Key space）與一個 Bit $b \leftarrow \{0, 1\}$。接著提取器建立一個空列表 $\Gamma$，而當 $\mathcal{A}$ 使用 Random Oracle（$H$）時，此提取器模擬該 Random Oracle，依照輸入值進行以下行為：如果 $s \neq \hat{s}$，提取器檢查 $(s, k’)$ 是否存在於 $\Gamma$，如果存在，回傳 $k’$，否則隨機選取 $k’$ 後存入 $\Gamma$ 並回傳；而如果 $s = \hat{s}$，則中斷 $\mathcal{A}$ 並回傳 $k$。

由於該攻擊者是在 AGM 下執行，考慮攻擊者的輸入：

$$
[\mathcal{X}]_1 = ([\alpha]_1, \{[ru_i(x)]_1\}_{i=0}^m) \\
[\mathcal{Y}]_2 = ([\beta]_2, \{[rv_i(x)]_2\}_{i=0}^m) \\
[\mathcal{Z}]_T = ( \{ [r\beta u_i(x) + r\alpha v_i(x) + r^2w_i(x)]_T \}^m_{i=\ell+1}, \{ [r^2 x^i t(x)]_T \}^{n-2}_{i=0})
$$

其中 $[\mathcal{Z}]_T$ 經由以下計算得到：

$$
[r\beta u_i(x) + r\alpha v_i(x) + r^2w_i(x)]_T = [\frac{r\beta u_i(x) + r\alpha v_i(x) + r^2w_i(x)}{\delta}]_1 \cdot [\delta]_2 \\
[r^2 x^i t(x)]_T = [\frac{r^2 x^i t(x)}{\delta}]_1 \cdot [\delta]_2
$$

攻擊者也將輸出向量：

$$
((\mathcal{A}_{i,j})_{i\in[m],j\in[m]}, (\mathcal{B}_{i})_{i\in[m-\ell-1+n-2]})
$$

我們注意到 $\mathcal{A}_{i.j}, \mathcal{B}_{i}$ 的對應關係。

$\mathcal{A}_{0,0}$ 相當於 $[\alpha]_1 \cdot [\beta]_2$ 的係數，固定為 1，${\mathcal{A}_{0,i}}_{i=0}^m$ 相當於 $B$ 計算中的 $\{a_i\}_{i=0}^m$（後面記為 $\{a_{B,i}\}_{i=0}^m$），$\{\mathcal{A}_{i,0}\}_{i=0}^m$ 相當於 $A$ 計算中的 $\{a_i\}_{i=0}^m$（後面記為 $\{a_{A,i}\}_{i=0}^m$），其餘部分則是 $a_{A,i}a_{B,i}$，後續不會用到因此跳過。

$\{\mathcal{B}_{i}\}_{i=0}^{m-\ell-1}$ 相當於 $C$ 計算中的 $\{a_i\}_{i=\ell+1}^m$（後面記為 $\{a_{C,i}\}_{i=\ell+1}^m$）。$\{\mathcal{B}_{i}\}_{i=m-\ell}^{m-\ell-1+n-2}$ 則是相當於 $h(x)$ 的係數。

WKEM 等式推導

而從 Encap 演算法的 $s$ 與攻擊者的 $s$ 相等，我們可以得到以下等式：

$$
\begin{align*}
s = &[\alpha]_1 \cdot [\beta]_2 + \sum^\ell_{i=0} a_i[r\beta u_i(x) + r\alpha v_i(x) + r^2w_i(x)]_1 \cdot [1]_2 \\
= &([\alpha]_1 + \sum^{m}_{i=0}a_{A,i} [ru_i(x)]_1) \cdot ([\beta]_2 + \sum^{m}_{i=0}a_{B,i} [rv_i(x)]_2) \\
& - (\sum^{m}_{i=\ell+1}a_{C,i}[\frac{r\beta u_i(x) + r\alpha v_i(x)+r^2w_i(x)}{\delta}]_1 + [\frac{r^2h(x)t(x)}{\delta}]_1) \cdot [\delta]_2
\end{align*}
$$

化簡後可得：

$$
\begin{align*}
\sum^\ell_{i=0} & a_i[r\beta u_i(x) + r\alpha v_i(x) + r^2w_i(x)]_1 \cdot [1]_2 \\
= \sum^{m}_{i=0} & a_{A,i} [ru_i(x)]_1 \cdot [\beta]_2 + \sum^{m}_{i=0} a_{B,i} [\alpha]_1 \cdot [rv_i(x)]_2 \\
& + (\sum^{m}_{i=0}a_{A,i} [ru_i(x)]_1) \cdot (\sum^{m}_{i=0}a_{B,i} [rv_i(x)]_2) \\
& - (\sum^{m}_{i=\ell+1}a_{C,i}[\frac{r\beta u_i(x) + r\alpha v_i(x)+r^2w_i(x)}{\delta}]_1 + [\frac{r^2h(x)t(x)}{\delta}]_1) \cdot [\delta]_2
\end{align*}
$$

將雙邊都計算出 $\mathbb{G}_T$ 的值：

$$
\begin{align*}
\sum^\ell_{i=0} & a_i[r\beta u_i(x) + r\alpha v_i(x) + r^2w_i(x)]_T \\
= \sum^{m}_{i=0} & a_{A,i} [r\beta u_i(x)]_T + \sum^{m}_{i=0} a_{B,i} [r\alpha v_i(x)]_T \\
& + [\sum^{m}_{i=0}a_{A,i} ru_i(x) \sum^{m}_{i=0}a_{B,i} rv_i(x)]_T \\
& - (\sum^{m}_{i=\ell+1}a_{C,i}[r\beta u_i(x) + r\alpha v_i(x)+r^2w_i(x)]_T + [r^2h(x)t(x)]_T)
\end{align*}
$$

整理等式，將包含 $w(x)$ 的移到右側，不包含的移到左側，並雙邊同除 $r^2$：

$$
\begin{align*}
[\sum^{m}_{i=0} & a_{A,i} u_i(x) \sum^{m}_{i=0}a_{B,i} v_i(x)]_T \\
& + \sum^{m}_{i=0} a_{A,i} [\frac{\beta u_i(x)}{r}]_T + \sum^{m}_{i=0} a_{B,i} [\frac{\alpha v_i(x)}{r}]_2 \\
= \sum^\ell_{i=0} & a_i[\frac{\beta u_i(x)}{r} + \frac{\alpha v_i(x)}{r} + w_i(x)]_T \\
& + (\sum^{m}_{i=\ell+1}a_{C,i}[\frac{\beta u_i(x)}{r} + \frac{\alpha v_i(x)}{r}+w_i(x)]_T + [h(x)t(x)]_T)
\end{align*}
$$

我們觀察 $\frac{\alpha}{r}, \frac{\beta}{r}$，可以發現該值不等於 0，且其係數與其他項無關，因此我們可以得知：

$$
\sum^{m}_{i=0} a_{A,i} u_i(x) - \sum^{\ell}_{i=0} a_{i} u_i(x) - \sum^{m}_{i=\ell+1} a_{C,i} u_i(x) = 0 \\
\sum^{m}_{i=0} a_{B,i} v_i(x) - \sum^{\ell}_{i=0} a_{i} v_i(x) - \sum^{m}_{i=\ell+1} a_{C,i} v_i(x) = 0
$$

我們也可以再進一步整理前一步的式子，得到：

$$
\begin{align*}
[\sum^{m}_{i=0} & a_{A,i} u_i(x) \sum^{m}_{i=0}a_{B,i} v_i(x)]_T \\
& = \sum^\ell_{i=0} a_i[w_i(x)]_T + (\sum^{m}_{i=\ell+1}a_{C,i}[w_i(x)]_T + [h(x)t(x)]_T)
\end{align*}
$$

提取器建構 Groth16 證明

當提取器自攻擊者取得這些係數後，可以建構一個 Groth16 Proof $[A’]_1, [B’]_2, [C’]_1$

$$
\begin{align*}
A’ &= \alpha + \sum_{i=0}^m a_{A,i} u_i(x) + r’ \delta’ \\
B’ &= \beta + \sum_{i=0}^m a_{B,i} v_i(x) + s’ \delta’ \\
C’ &= \sum_{i=\ell+1}^m \frac{ a_{C,i} (\beta u_i(x) + \alpha v_i(x) + w_i(x)) + h(x) t(x)}{\delta’} + s’A + r’B - r’s’\delta’
\end{align*}
$$

此處 $r’, s’, \delta’$ 是來自於 $\sigma_\text{Groth16}$。我們將此三元素帶入 Groth16 的 Verify 演算法：

$$
\begin{align*}
[A’]_1 \cdot &[B’]_2 = \\
& [\alpha]_1 \cdot [\beta]_2 + \sum_{i=0}^{\ell} a_i \left[ \frac{\beta u_i(x) + \alpha v_i(x) + w_i(x)}{\gamma} \right]_1 \cdot [\gamma]_2 + [C’]_1 \cdot [\delta’]_2
\end{align*}
$$

展開後得：（為避免式子過長，最後一行的在此不展開，簡言之該行消除了 $A’, B’$ 中的 $r’\delta’, s’\delta’$ 部分。）

$$
\begin{align*}
([\alpha]_1 + & \sum_{i=0}^m a_{A,i} [u_i(x)]_1 + r [\delta’]_1) \cdot ([\beta]_2 + \sum_{i=0}^m a_{B,i} [v_i(x)]_2 + s [\delta’]_2) = \\
[\alpha]_1 &\cdot [\beta]_2 + \sum_{i=0}^{\ell} a_i \left[ \frac{\beta u_i(x) + \alpha v_i(x) + w_i(x)}{\gamma} \right]_1 \cdot [\gamma]_2 \\
& + (\sum_{i=\ell+1}^m [\frac{ a_{C,i} (\beta u_i(x) + \alpha v_i(x) + w_i(x)) + h(x) t(x)}{\delta}]_1) \cdot [\delta’]_2 \\
& + (s’[A]_1 + r’[B]_1 - [r’s’\delta’]_1) \cdot [\delta’]_2
\end{align*}
$$

左右消除相等值後得：

$$
\begin{align*}
(\sum_{i=0}^m a_{A,i} & [u_i(x)]_1) \cdot (\sum_{i=0}^m a_{B,i}[v_i(x)]_2) \\
& + \sum_{i=0}^m a_{B,i} [\alpha]_1 \cdot [v_i(x)]_2 + \sum_{i=0}^m a_{A,i} [u_i(x)]_1 \cdot [\beta]_2 = \\
\sum_{i=0}^{\ell} a_i & \left[ \frac{\beta u_i(x) + \alpha v_i(x) + w_i(x)}{\gamma} \right]_1 \cdot [\gamma]_2 \\
& + (\sum_{i=\ell+1}^m [\frac{ a_{C,i} (\beta u_i(x) + \alpha v_i(x) + w_i(x)) + h(x) t(x)}{\delta}]_1) \cdot [\delta’]_2
\end{align*}
$$

將雙邊都計算出 $\mathbb{G}_T$ 的值：

$$
\begin{align*}
[\sum_{i=0}^m & a_{A,i} u_i(x) \sum_{i=0}^m a_{B,i}v_i(x)]_T + \sum_{i=0}^m a_{B,i} [\alpha v_i(x)]_T + \sum_{i=0}^m a_{A,i} [\beta u_i(x)]_T \\
= & \sum_{i=0}^{\ell} a_i \left[ \beta u_i(x) + \alpha v_i(x) + w_i(x) \right]_T \\
& + \sum_{i=\ell+1}^m [a_{C,i} (\beta u_i(x) + \alpha v_i(x) + w_i(x)) + h(x) t(x)]_T
\end{align*}
$$

在 WKEM-等式推導 段落中，我們知道：

$$
\sum^{m}_{i=0} a_{A,i} u_i(x) - \sum^{\ell}_{i=0} a_{i} u_i(x) - \sum^{m}_{i=\ell+1} a_{C,i} u_i(x) = 0 \\
\sum^{m}_{i=0} a_{B,i} v_i(x) - \sum^{\ell}_{i=0} a_{i} v_i(x) - \sum^{m}_{i=\ell+1} a_{C,i} v_i(x) = 0
$$

代入式子，可以將具有 $\alpha, \beta$ 的部分清除：

$$
\begin{align*}
[\sum_{i=0}^m & a_{A,i} u_i(x) \sum_{i=0}^m a_{B,i}v_i(x)]_T \\
= & \sum_{i=0}^{\ell} a_i \left[w_i(x) \right]_T + \sum_{i=\ell+1}^m [a_{C,i} w_i(x) + h(x) t(x)]_T
\end{align*}
$$

而在 WKEM-等式推導 段落，我們已經驗證此等式成立，因此該 Proof 將通過 Groth16 的 Verify 演算法，使之輸出 1。

Groth16 安全性到 WKEM 安全性

由於該 Proof，有效，根據 Soundness 定義，從該證明無法提取出 $w$ 使 $({a_i}_{i=0}^{\ell}, {a_i}_{i=\ell+1}^{m}) \in R$ 的機率可忽略。我們使 WKEM 的提取器輸出 Groth16 提取器的 $w$，可得：

$$
\text{Pr}\left[
(\{a_i\}_{i=0}^{\ell}, \{a_i\}_{i=\ell+1}^{m}) \in R :
\begin{array}{r}
\{a_i\}_{i=0}^{\ell} \leftarrow \mathcal{A}(1^\lambda, R) \\
\{a_i\}_{i=\ell+1}^{m} \leftarrow \text{Ext}^{\mathcal{A}(\cdot, \cdot)}(R, \{a_i\}_{i=0}^{\ell})
\end{array}
\right] \\
= 1 - \text{negl}_{CKS}(\lambda) \geq \delta(\lambda)
$$

因此我們的安全性滿足定義。

結論

本研究基於 zkSNARK 中經常被使用到的 QAP 設計，自 Groth16 提出以來，已經有如 Circom 等知名的專案能夠幫助開發者將程式轉換成 QAP。我們基於 Groth16 的架構，設計出一個 WKEM-WE 方案，從而使得這些既有工具能夠直接被使用，這使得我們的方案有更高的可實現性。

然而考慮到量子電腦的發展，且與 Groth16 相同，我們的方案並不抗量子。另一面，zkSNARK 近年也有許多抗量子設計，因此我們本研究的方式或許可以應用到其他方案，進而提出抗量子且可實現的 Witness Encryption 方案。